Chứng minh rằng hình chóp đều có các mặt bên là những tam giác cân bằng nhau

* Hướng dẫn giải

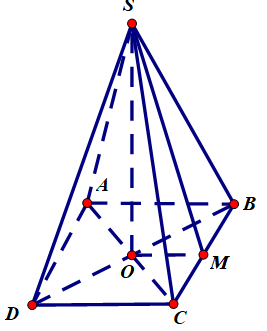
Xét trường hợp Hình chóp tứ giác đều

Ta có đáy là hình vuông ABCD

Tâm hình vuông ABCD là O (giao điểm 2 đường chéo)

Gọi M là trung điểm BC ⇒ OM // AB hay OM ⊥ BC

Theo định nghĩa hình chóp đều, SO ⊥ (ABCD) ⇒ SO ⊥ BC

⇒ BC ⊥(SO,OM) ⇒ BC⊥(SOM) ⇒ BC⊥SM

Tam giác SBC có SM vừa là đường cao vừa là trung tuyến ⇒ SBC cân tại S

Chứng minh tương tự ⇒ Các mặt bên là những tam giác cân bằng nhau

Trường hợp hình chóp đều khác, chứng minh tương tự