Trang chủ
Đề thi & kiểm tra
Lớp 11
Toán học
Giải toán 11: Hình học !!
Cho tứ diện đều ABCD. Gọi M, N lần lượt...
Cho tứ diện đều ABCD. Gọi M, N lần lượt là trung điểm của cạnh BC và AD
Câu hỏi :
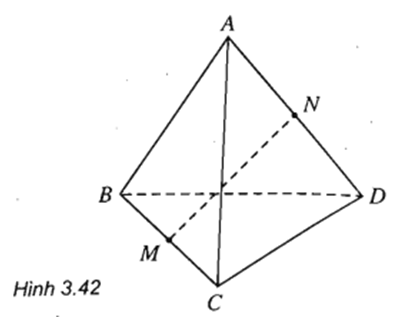
Cho tứ diện đều ABCD. Gọi M, N lần lượt là trung điểm của cạnh BC và AD. Chứng minh rằng: MN ⊥ BC và MN ⊥ AD (h.3.42)
* Đáp án
* Hướng dẫn giải
Tứ diện đều ABCD nên các mặt của tứ diện là các tam giác đều bằng nhau
Ta có: ∆BAD = ∆CAD (c.c.c)
Suy ra hai đường trung tuyến tương ứng bằng nhau: BN = CN
⇒ ΔBNC cân tại N.
Do NM là đường trung tuyến của tam giác cân BNC nên NM đồng thời là đường cao:
⇒ MN ⊥ BC
Chứng minh tương tự MN ⊥ AD
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải toán 11: Hình học !!
Số câu hỏi: 209
Copyright © 2021 HOCTAP247