Chứng minh phương trình luôn x^n + a1x^(n-1) + a2x^(n-2) +...+ a(n-1)x + an = 0

* Hướng dẫn giải

Hàm số $f\left(x\right) = x^n + a_1{x}^{n-1} + a_2{x}^{n-2} + ... + a_{n-1}x + a_n = 0$ xác định trên R

- Ta có

Vì 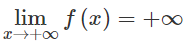 nên với dãy số $\left(x_n\right)$ bất kì mà $x_n \to +\infty$ ta luôn có lim $f\left(x_n\right) = +\infty$

Do đó, $f\left(x_n\right)$ có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.

Nếu số dương này là 1 thì $f\left(x_n\right) > 1$ kể từ một số hạng nào đó trở đi.

Nói cách khác, luôn tồn tại số a sao cho f(a) > 1 (1)

Vì 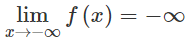 nên với dãy số $\left(x_n\right)$ bất kì mà $x_n \to -\infty$ ta luôn có lim $f\left(x_n\right) = -\infty$ hay $lim[-f(x_n\left)\right] = +\infty$

Do đó, $-f\left(x_n\right)$ có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.

Nếu số dương này là 1 thì $-f\left(x_n\right) > 1$ kể từ số hạng nào đó trở đi. Nói cách khác, luôn tồn tại b sao cho −f(b) > 1 hay f(b) < −1 (2)

- Từ (1) và (2) suy ra f(a).f(b) < 0

Mặt khác, f(x) hàm đa thức liên tục trên R nên liên tục trên [a; b]

Do đó, phương trình f(x) = 0 luôn có nghiệm.