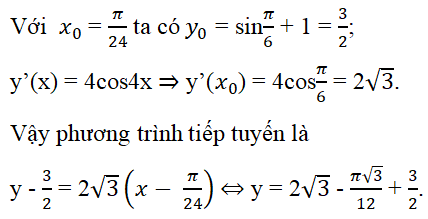Cho hàm số y = sin4x Chứng minh rằng sin4(x + kπ/2) = sin4x

* Hướng dẫn giải

a) Ta có sin4(x + kπ/2) = sin(4x + k2π) = sin4x với k ∈ Z.

Từ đó suy ra hàm số y = sin4x là hàm số tuần hoàn với chu kì π/2.

Vì hàm số y = sin4x là hàm số lẻ nên đồ thị của nó có tâm đối xứng là gốc tọa độ O.

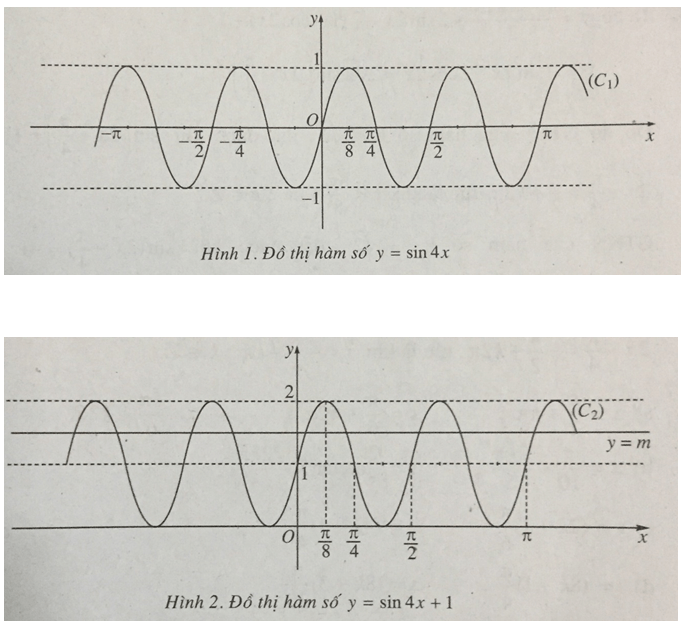
Các hàm số y = sin4x (C1) và y = sin4x + 1 (C2) có đồ thị như trên hình 1 và hình 2.

b) Vì sin4x + 1 = m ⇔ sin4x = m – 1

và -1 ≤ sin4x ≤ 1

nên -1 ≤ m – 1 ≤ 1

⇔ 0 ≤ m ≤ 2.

Từ đó, phương trình (1) có nghiệm khi 0 ≤ m ≤ 2 và vô nghiệm khi m > 2 hoặc m < 0.

c) Phương trình tiếp tuyến của (C2) có dạng

$y - y_o = y’\left(x_o\right)(x - x_o)$.