Trang chủ
Đề thi & kiểm tra
Lớp 11
Toán học
Giải sách bài tập Hình học 11 !!
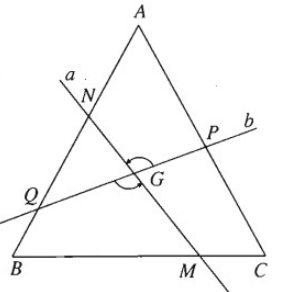
Qua tâm G của tam giác đều ABC, kẻ đường...
Qua tâm G của tam giác đều ABC, kẻ đường thẳng a cắt BC tại M và cắt AB
Câu hỏi :
Qua tâm G của tam giác đều ABC, kẻ đường thẳng a cắt BC tại M và cắt AB tại N, kẻ đường thẳng b cắt AC tại P và AB tại Q, đồng thời góc giữa a và b bằng . Chứng minh rằng tứ giác MNPQ là một hình thang cân.
* Đáp án
* Hướng dẫn giải
Gọi là phép quay tâm G góc . Phép quay này biến b thành a, biến CA thành AB; do đó nó biến P thành N.
Tương tự cũng biến Q thành M. Từ đó suy ra GP = GN, GQ = GM. Do đó hai tam giác GNQ và GPM bằng nhau, suy ra NQ = PM. Vì biến PQ thành NM nên PQ = NM. Từ đó suy ra hai tam giác NQM và PMQ bằng nhau. Do đó ∠NQM = ∠PMQ. Tương tự ∠QNP = ∠MPN.
Từ đó suy ra
Do đó NP // QM. Vậy ta có tứ giác MPNQ là hình thang cân.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải sách bài tập Hình học 11 !!
Số câu hỏi: 159
Copyright © 2021 HOCTAP247