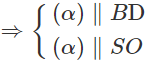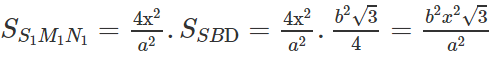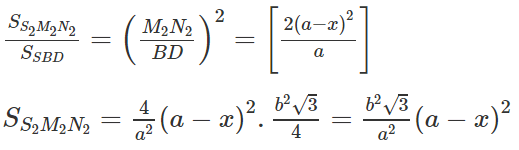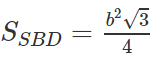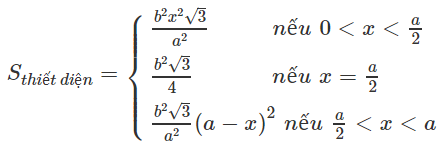Cho hình chóp S.ABCD có đáy là hình bình hành ABCD, O là giao điểm hai đường chéo
Câu hỏi :
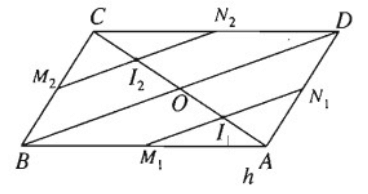
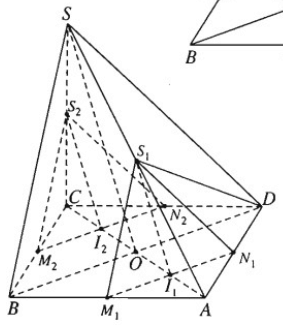
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD, O là giao điểm hai đường chéo, AC = a, BD = b, tam giác SBD đều. Gọi I là điểm di động trên đoạn AC với AI = x (0 < 0 < a). Lấy là mặt phẳng đi qua I và song song với mặt phẳng (SBD).
* Đáp án
* Hướng dẫn giải
a) Trường hợp 1 .
I thuộc đoạn AO (0 < x < a/2)
Khi đó I ở vị trí I1
Ta có: (α) // (SBD)
Vì (α) // BD nên (α) cắt (ABD) theo giao tuyến M1N1 ( qua I1) song song với BD
Tương tự (α) // SO nên (α) cắt (SOA) theo giao tuyến
S1T1 song song với SO.
Ta có thiết diện trong trường hợp này là tam giác S1M1N1.
Nhận xét. Dễ thấy rằng . Lúc đó tam giác S1M1N1 đều.
Trường hợp 2. I thuộc đoạn OC (a/2 < x < a)
Khi đó I ở vị trí I2. Tương tự như trường hợp 1 ta có thiết diện là tam giác đều
, .
Trường hợp 3. I ≡ O. Thiết diện chính là tam giác đều SBD.
b) Ta lần lượt tìm diện tích thiết diện trong các trường hợp 1,2,3.
Trường hợp 1. I thuộc đoạn AO (0 < x < a/2)
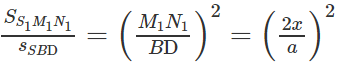
Trường hợp 2. I thuộc đoạn OC (a/2 < x < a)
Trường hợp 3. I ≡ O.
Tóm lại
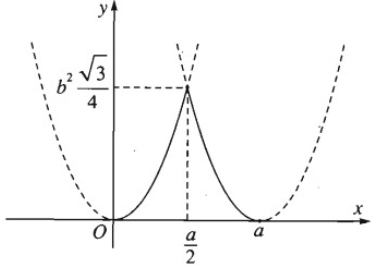
∗ Đồ thị của hàm số S theo biến x như sau:
Vậy Sthiết diện lớn nhất khi và chỉ khi x = a/2.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải sách bài tập Hình học 11 !!
Copyright © 2021 HOCTAP247