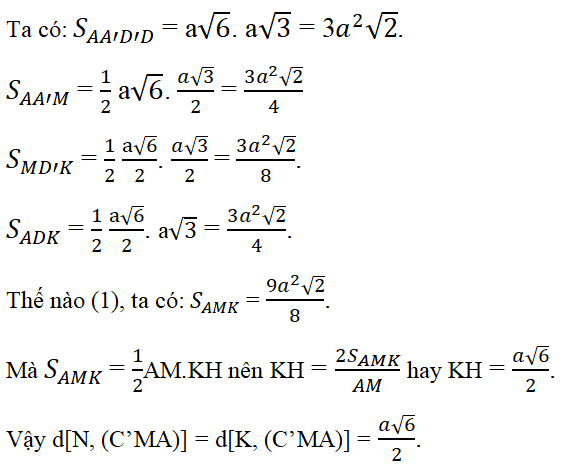Trang chủ
Đề thi & kiểm tra
Lớp 11
Toán học
Giải sách bài tập Hình học 11 !!
Cho lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình thoi,...
Cho lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình thoi, AB = a căn 3
Câu hỏi :
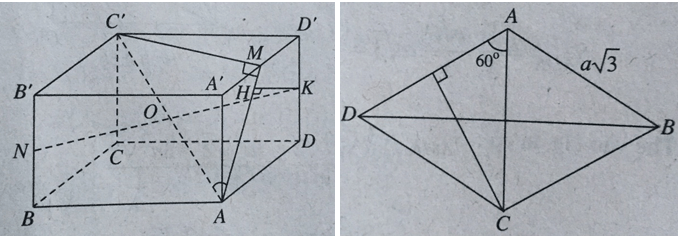
Cho lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình thoi, AB = a√3, . Góc giữa đường thẳng AC' và mặt phẳng (ADD'A') là . Gọi M là trung điểm A'D', N là trung điểm BB'. Tính khoảng cách từ N đến mặt phẳng (C'MA)
* Đáp án
* Hướng dẫn giải
Nhận xét:
Do tam giác A’B’D’ là tam giác đều nên C’M ⊥ A’D’
(C'A'D') ⊥ (AA'D'D) & (C'A'D') ∩(AA'D'D) ⇒ C’M ⊥ (AA’D’D)
Nên ∠(AC',(AA'D'D)) = ∠(C'AM) = .
Gọi K là trung điểm của DD’, ta có AKC’N là hình bình hành nên K với N đối xứng nhau qua trung điểm O của AC’. Mà O ∈ (AMC’), do đó
d[N,(C'MA)] = d[K,(C'MA)]
+ Xác định khoảng cách từ K đến (C’MA).
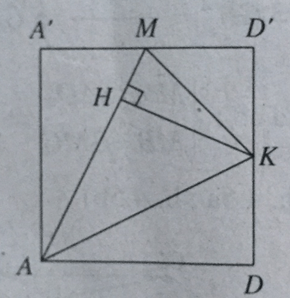
Do (C’MA) vuông góc với (AA’D’D) theo giao tuyến AM nên kẻ KH ⊥ AM, ta có KH ⊥ (C’MA) hay d[K,(C'MA)] = KH.
+ Tính KH.
Ta có: SAMK = SAA'D'D – (SAA'M + SMD'K + SADK) (1)
Trong tam giác AMC’, ta có: .
Trong tam giác AA’M, ta có: .
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải sách bài tập Hình học 11 !!
Số câu hỏi: 159
Copyright © 2021 HOCTAP247