Trang chủ
Đề thi & kiểm tra
Lớp 11
Toán học
Đề ôn tập Chương 3 Hình học lớp 11 năm 2021 Trường THPT Trần Hưng Đạo
Cho hình lăng trụ tam giác \(ABC.{A_1}{B_1}{C_1}\) có cạnh bên...
Cho hình lăng trụ tam giác \(ABC.{A_1}{B_1}{C_1}\) có cạnh bên bằng a.
Câu hỏi :
Cho hình lăng trụ tam giác \(ABC.{A_1}{B_1}{C_1}\) có cạnh bên bằng a. Các cạnh bên của lăng trụ tạo với mặt đáy góc 60o. Hình chiếu vuông góc của A lên mặt phẳng \(\left( {{A_1}{B_1}{C_1}} \right)\) là trung điểm của \({B_1}{C_1}.\) Khoảng cách giữa hai mặt đáy của lăng trụ bằng bao nhiêu?
A. \(a\frac{{\sqrt 3 }}{2}.\)
B. \(\frac{a}{3}.\)
C. \(a\frac{{\sqrt 2 }}{2}.\)
D. \(\frac{a}{2}.\)
* Đáp án
A
* Hướng dẫn giải
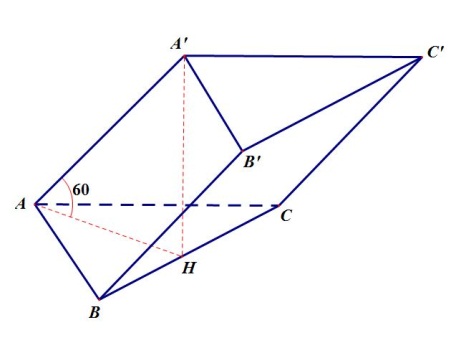
Ta có: \(A'H \bot \left( {ABC} \right) \to \widehat {A'AH} = {60^{\rm{o}}}.\)
\(d\left( {\left( {A'B'C'} \right),\left( {ABC} \right)} \right) = A'H = A'A.cos{60^{\rm{o}}} = a\frac{{\sqrt 3 }}{2}.\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề ôn tập Chương 3 Hình học lớp 11 năm 2021 Trường THPT Trần Hưng Đạo
Số câu hỏi: 38
Copyright © 2021 HOCTAP247
