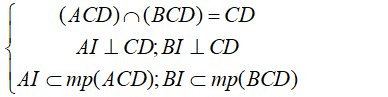Trang chủ
Đề thi & kiểm tra
Lớp 11
Toán học
Top 4 Đề kiểm tra 15 phút Toán 11 Chương 3 Hình học có đáp án !!
Cho tứ diện ABCD có AC = AD và BC...
Cho tứ diện ABCD có AC = AD và BC = BD. Gọi I là trung điểm của CD
Câu hỏi :
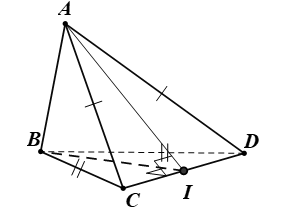
Cho tứ diện ABCD có AC = AD và BC = BD. Gọi I là trung điểm của CD. Chứng minh: Góc giữa hai mặt phẳng (ACD) và (BCD) là
* Đáp án
* Hướng dẫn giải
+) Tam giác BCD có BC = BD nên tam giác BCD cân tại B.
- Do BI là đường trung tuyến nên đồng thời là đường cao: CD ⊥ BI (1)
+) Tam giác ACD có AC = AD nên tam giác ACD cân tại A.
- Do AI là đường trung tuyến nên đồng thời là đường cao: CD ⊥ AI (2)
- Từ (1) và (2) ⇒ CD ⊥ (ABI).
- Ta có:
- Suy ra góc giữa hai mặt phẳng (ACD) và (BCD) là
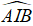
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Top 4 Đề kiểm tra 15 phút Toán 11 Chương 3 Hình học có đáp án !!
Số câu hỏi: 18
Copyright © 2021 HOCTAP247