Cho hình chóp S.ABCD có SA vuông góc với (ABCD), tứ giác ABCD là
Câu hỏi :
Cho hình chóp S.ABCD có SA ⊥ (ABCD), tứ giác ABCD là hình thang cân có đáy lớn AD gấp đôi đáy nhỏ BC và cạnh bên AB = BC. Mặt phẳng (P) đi qua A, vuông góc với SD và cắt SB, SC, SD lần lượt tại M, N, P. Khi đó ta có thể kết luận gì về tứ giác AMNP?
A. AMNP là một tứ giác nội tiếp (không có cặp cạnh đối nào song song).
B. AMNP là một hình thang vuông.
C. AMNP là một hình thang.
D. AMNP là một hình chữ nhật.
* Đáp án
A
* Hướng dẫn giải
Chọn A.
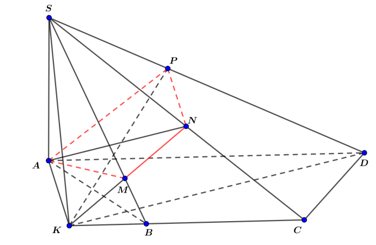
- Dựng AP ⊥ SD (P ∈ SD).
- Trong mp(SCD) dựng PN ⊥ SD (N ∈ SC)
- Khi đó mặt phẳng (P) ≡ (APN).
- Trong mặt phẳng (ABCD) dựng AK ⊥ AD (K ∈ BC).
- Mà: AK ⊥ SA ⇒ AK ⊥ SD ⇒ K ∈ (APN).
- Trong (SBC) , gọi M = NK ∩ SB. Khi đó tứ giác AMNP là thiết diện của mặt phẳng (P) với hình chóp S.ABCD suy ra tứ giác AMNP nội tiếp đường tròn.
Cách khác:
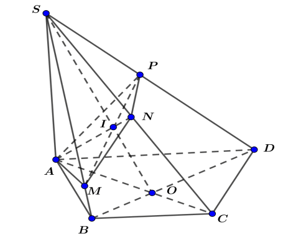
- Dựng AP ⊥ SD (P ∈ SD).
- Trong (SCD) dựng PN ⊥ SD (N ∈ SC).
- Khi đó mặt phẳng (P) ≡ (APN).
- Trong (ABCD), gọi O = AC ∩ BD.
- Trong (SAC), gọi I = AC ∩ SO.
- Trong (SBD), gọi M = PI ∩ SB.
- Khi đó mặt phẳng (P) ≡ (AMNP).
- Ta có: IA.IN = IP.IM ⇒ AMNP nội tiếp đường tròn.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Top 4 Đề thi Toán 11 Học kì 2 có đáp án !!
Copyright © 2021 HOCTAP247