Trong thí nghiệm giao thoa sóng mặt nước, hai nguồn sóng S_1 và S_2 cách nhau

Câu hỏi :

Trong thí nghiệm giao thoa sóng mặt nước, hai nguồn sóng ${S_1}$ và ${S_2}$ cách nhau 11cm và dao động điều hòa theo phương vuông góc với mặt nước có cùng phương trình ${u_1}$ = ${u_2}$ = 5cos100πt (mm). Tốc độ truyền sóng v = 0,5 m/s và biên độ sóng không đổi khi truyền đi. Chọn hệ chục xOy thuộc mặt phẳng mặt nước khi yên lặng, gốc O trùng với ${S_1}$, Ox trùng ${S_1}{S_2}$. Trong không gian, phía trên mặt nước có 1 chất điểm chuyển động mà hình chiếu (P) của nó với mặt nước chuyển động với phương trình quỹ đạo y = x + 2 và có tốc độ v = 5√2 cm/s. Trong thời gian t = 2 s kể từ lúc (P) có tọa độ x = 0 thì (P) cắt bao nhiêu vân cực đại trong vùng giao thoa sóng ?

* Đáp án

D

* Hướng dẫn giải

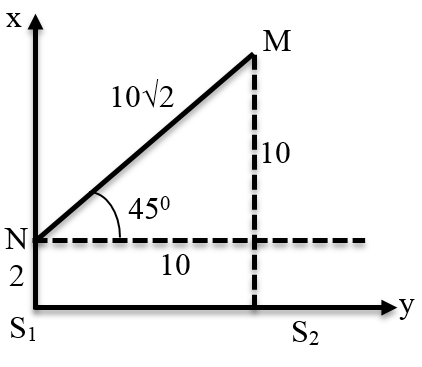
Ta có λ = 1 cm.
Quãng đường (P) đi được trong 2 s là 10√2 cm.
Ta có: $\left\{ \begin{array}{l}
N{S_2} - N{S_1} = \sqrt {{2^2} + {{11}^2}} - 2 = 5\sqrt 5 - 2 \approx 9,1\\
M{S_2} - M{S_1} = \sqrt {{{\left( {11 - 10} \right)}^2} + {{\left( {0 - 12} \right)}^2}} - \sqrt {{{10}^2} + {{12}^2}} \approx - 3,57
\end{array} \right.$
Suy ra $M{S_2} - M{S_1} \le k\lambda \le N{S_2} - N{S_1}$.
Ta tìm được 13 giá trị của k.