Trang chủ
Đề thi & kiểm tra
Vật lý
Đề ôn luyện thi THPT Quốc gia môn Lý số 1 có đáp án
Cho mạch điện AMNB, trong đó giữa A và M,...
Cho mạch điện AMNB, trong đó giữa A và M, giữa M và N, giữa N và B lần lượt là
Câu hỏi :
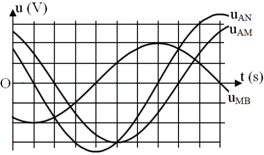
Cho mạch điện AMNB, trong đó giữa A và M, giữa M và N, giữa N và B lần lượt là tụ điện C, điện trở R, cuộn cảm thuần L. Khi đặt vào hai đầu AB một điện áp có giá trị hiệu dụng và tần số ổn định thì điện áp giữa hai điểm A và M, A và N, M và B lần lượt là u$_{AM}$, u$_{AN}$, u$_{MB}$. Trong cùng một hệ trục tọa độ Out, các điện áp u$_{AM}$, u$_{AN}$, u$_{MB}$ được biểu diễn như hình vẽ bên. Tính tỉ số Z$_L$/Z$_C$ giữa cảm kháng của cuộn cảm và dung kháng của tụ điện
A. 2/5
B. 1/5
C. 1/3
D. 2/3
* Đáp án
C
* Hướng dẫn giải
Ta giả sử 1 đơn vị trên trục Ou là 1 V, 1 đơn vị trên trục Ot là 1 s.Chu kì dao động là 12 s.
Xét u$_{AM}$: tại t = 0 đến t = 2,0 s dao động qua VTCB theo chiều âm → u$_{AM}$ = 3cos(ωt + π/6).
Xét u$_{MB}$: tại t = 0 đến t = 1,0 s dao động qua vị trí biên âm → u$_{MB}$ = 2cos(ωt + 5π/6).
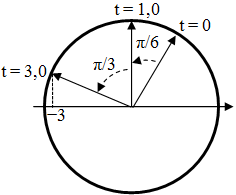
Xét u$_{AN}$: tại t = 0 đến t = 1,0 s dao động qua VTCB theo chiều âm → pha ban đầu là π/3.
tại t = 1,0 s vật qua VTCB theo chiều âm đếm t = 3,0 s, vật qua vị trí −3 V và đang giảm. Nên u$_{AN}$ = 2$\sqrt 3 $cos(ωt + π/3).
Vậy: $\frac{{{Z_L}}}{{{Z_C}}} = \left| {\frac{{{u_{NB}}}}{{{u_{AM}}}}} \right| = \left| {\frac{{{u_{AM}} + {u_{MB}} - {u_{AN}}}}{{{u_{AM}}}}} \right| = \left| {\frac{{3\angle \frac{\pi }{6} + 2\angle \frac{{5\pi }}{6} - 2\sqrt 3 \angle \frac{\pi }{3}}}{{3\angle \frac{\pi }{6}}}} \right| = \frac{1}{3}$.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề ôn luyện thi THPT Quốc gia môn Lý số 1 có đáp án
Số câu hỏi: 40
Copyright © 2021 HOCTAP247
