Bài 34 trang 80 SGK Toán 9 tập 2

Đề bài

Cho đường tròn \((O)\) và điểm \(M\) nằm bên ngoài đường tròn đó. Qua điểm \(M\) kẻ tiếp tuyến \(MT\) và cát tuyến \(MAB.\) Chứng minh \(MT^2  = MA. MB\).

Hướng dẫn giải

+) Trong một đường tròn, góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn một cung thì có số đo bằng nhau và bằng nửa số đo cung bị chắn.

+) Chứng minh cặp tam giác đồng dạng tương ứng. Từ đó suy ra các cặp tương ứng tỉ lệ và đẳng thức cần chứng minh.

Lời giải chi tiết

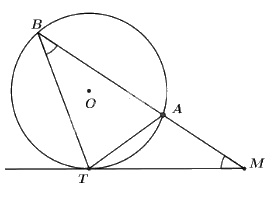
Xét hai tam giác \(BMT\)  và \(TMA\), chúng có:

\(\widehat{M}\) chung

\(\widehat{B} = \widehat{T}\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến cùng chắn cung nhỏ \(\overparen{AT}\))

\(\Rightarrow ∆BMT\) đồng dạng \(∆TMA \, (g-g).\)

\(\Rightarrow \frac{MT}{MA} =  \frac{MB}{MT}\) (các cặp cạnh tương ứng tỉ lệ).

hay \(MT^2  = MA. MB\) (đpcm).