Giải bài 34 trang 80 - Sách giáo khoa Toán 9 tập 2

Đề bài

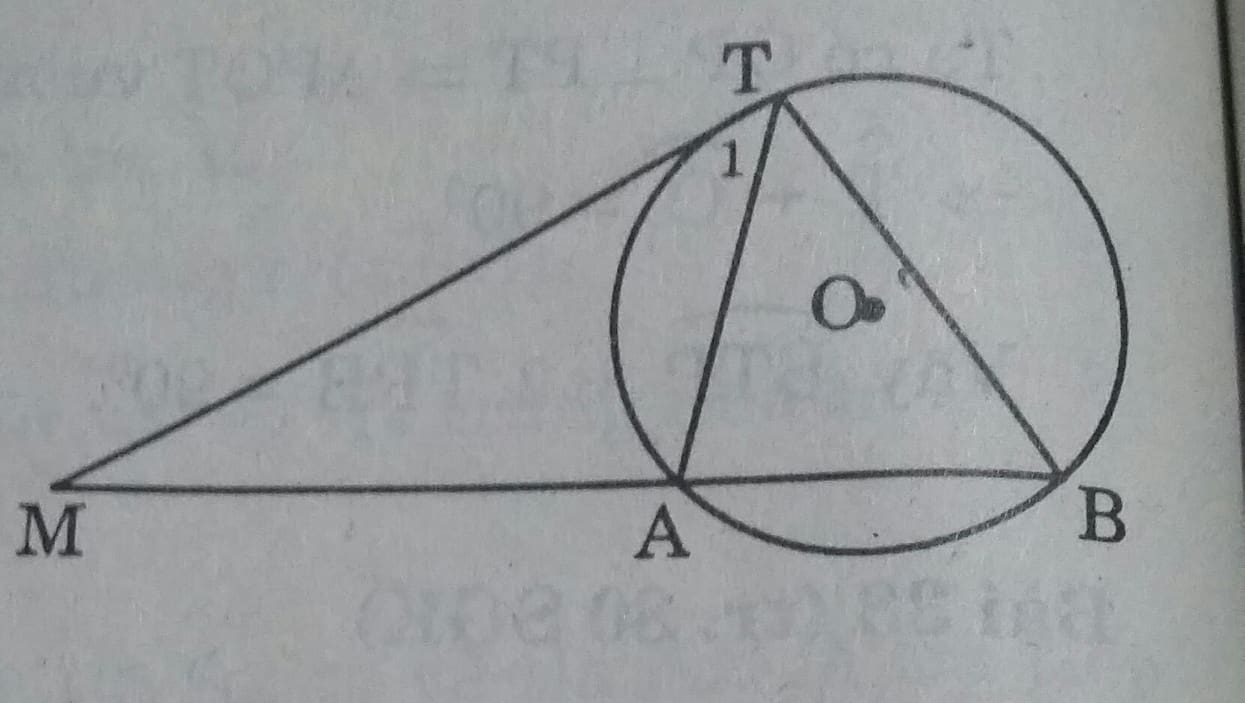
    Cho đường tròn (O) và điểm M nằm bên ngoài đường tròn đó. Qua điểm M kẻ tiếp tuyến MT và cát tuyến MAB.

Chứng minh \(MT^2 = MA.MB.\)

Hướng dẫn giải

   Xét \(\Delta MTA \ và \Delta MBT \ có . \widehat{M}\) chung \(\widehat{T_1}= \widehat{B}\)( góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung \(\stackrel\frown{AT}\))

   \( \Rightarrow \Delta MTA \approx \Delta MBT (g.g)\)

   \(\Rightarrow \dfrac{MT}{MB}= \dfrac{MA}{MT} \Rightarrow MT^ = MA.MB\)