Trang chủ
Lớp 9
Toán Lớp 9 SGK Cũ
Bài 4. Góc tạo bởi tia tiếp tuyến và dây cung
Giải bài 33 trang 80 - Sách giáo khoa Toán 9 tập 2
Giải bài 33 trang 80 - Sách giáo khoa Toán 9 tập 2
Lý thuyết
Bài tập
Mục lục
Tóm tắt bài
Đề bài
Cho A, B, C là ba điểm trên một đường tròn, At là tiếp tuyến của đường tròn tại A. Đường thẳng song song với At cắt AB tại M và cắt AC tại N. Chứng minh AB.AM = AC.AN.
Hướng dẫn giải
Ta có \(\widehat{A_1}= \widehat{C}\)( góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung \( \stackrel\frown{AB}\))
\(\widehat{A_1}= \widehat{M_1}\) ( hai góc so le trong)
Suy ra \(\widehat{M_1}= \widehat{C_1}\)
Xét \(\Delta AMN \ và \Delta ACB \ có:\)
\(\widehat{M_1}= \widehat{C}; \widehat{A} \ chung\)
\( \Rightarrow \Delta AMN \sim \Delta ACB(g.g)\)
\( \Rightarrow \dfrac{AM}{AC}=\dfrac{AN}{AB} \Rightarrow AM.AB= AN.AC\)
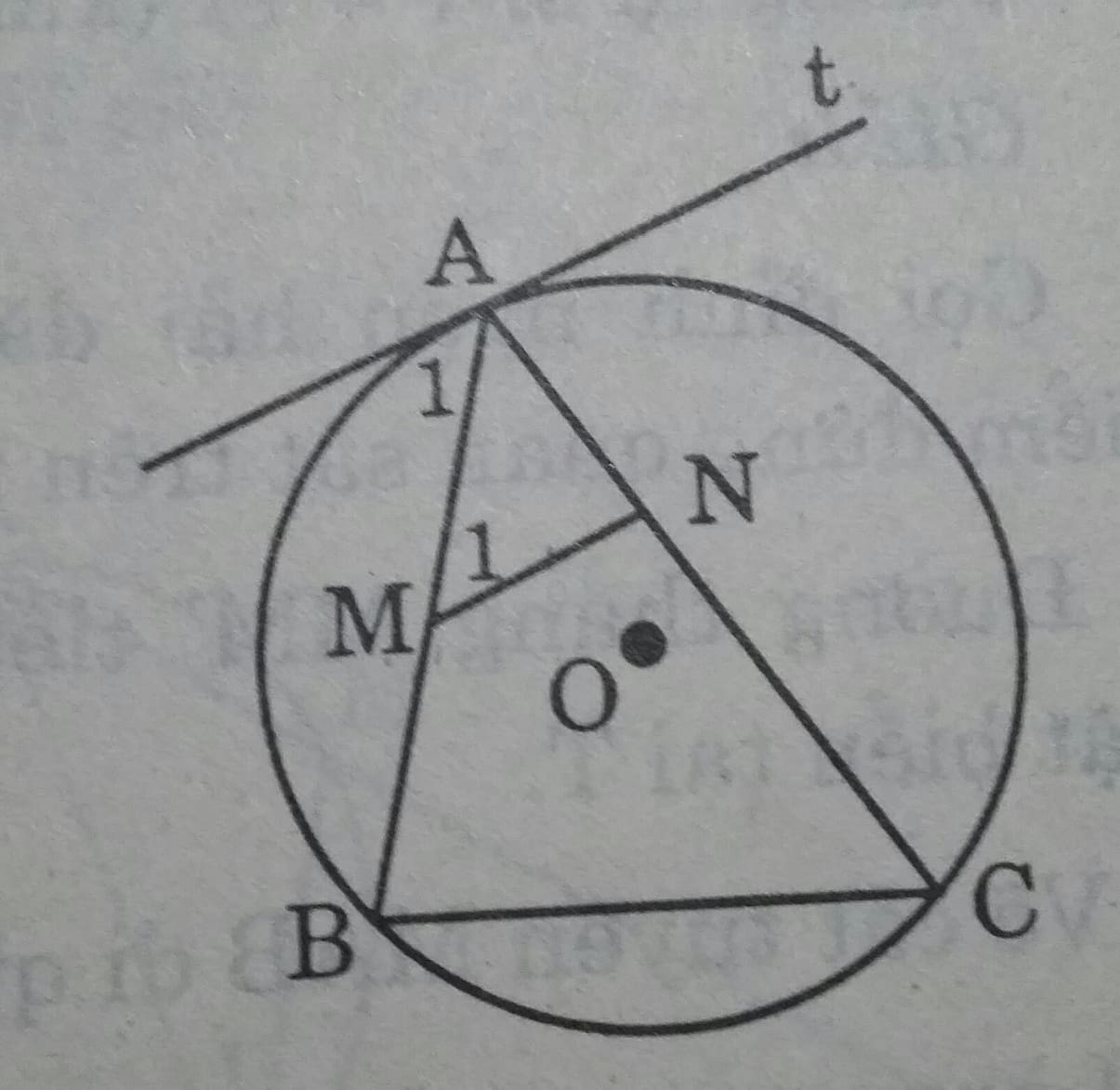
Copyright © 2021 HOCTAP247
