Giải bài 27 trang 79 - Sách giáo khoa Toán 9 tập 2

Đề bài

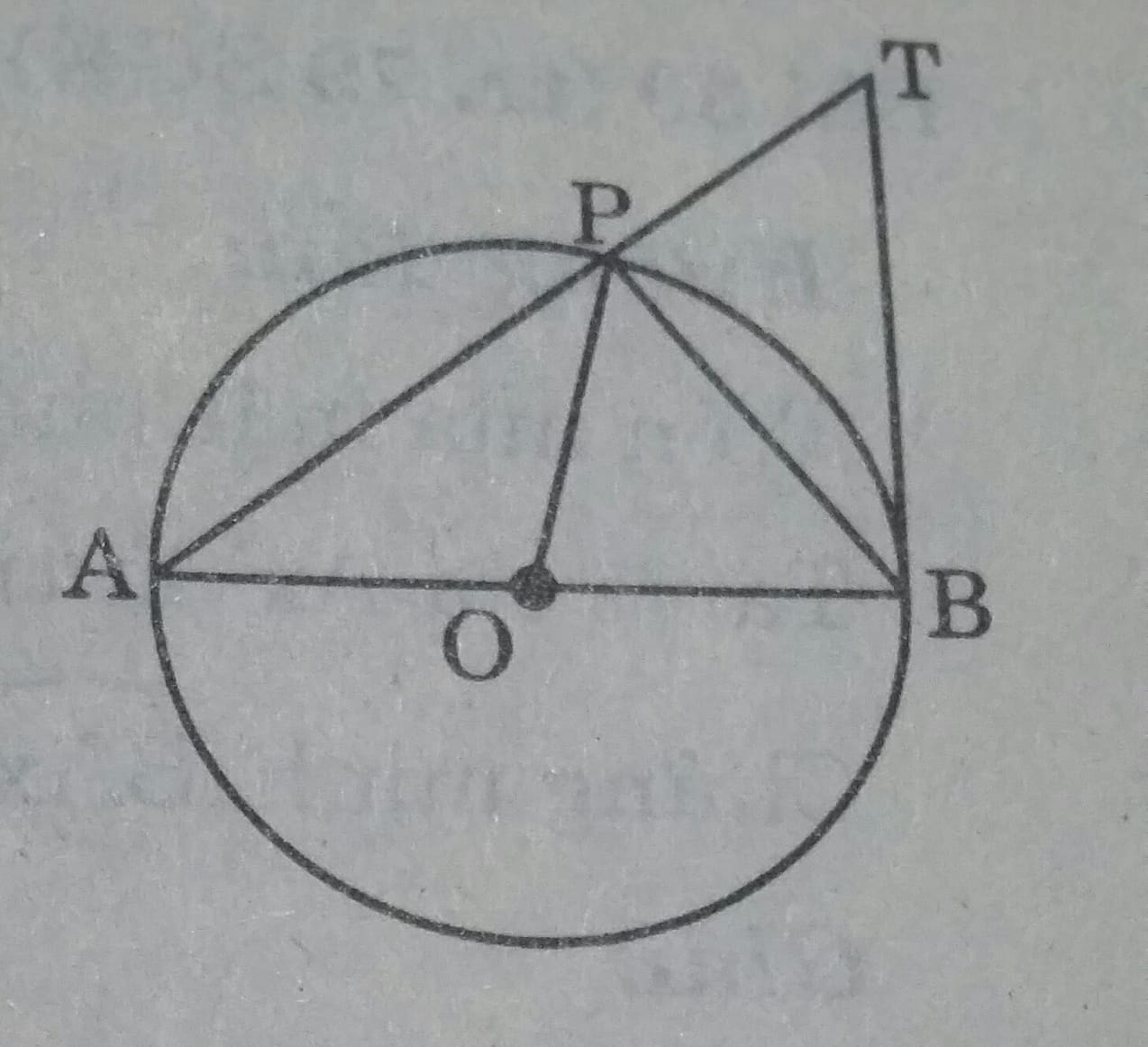
     Cho đường tròn tâm O, đường kính AB. Lấy điểm P khác A và B trên đường tròn. Gọi T là giao điểm của AP với tiếp tuyến tại B của đường tròn. Chứng minh

Hướng dẫn giải

   Ta có \(\widehat{APO}= \widehat{A}\) ( hai góc đáy của tam giác cân)

  \(\widehat{PBT}= \widehat{A}\)( góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung PB)

  \(\Rightarrow \widehat{APO}= \widehat{PBT}\)