Đề kiểm 15 phút - Đề số 5 - Bài 4 - Chương 3 - Hình học 9
Tóm tắt bài
Đề bài
Cho góc nhọn AMB nội tiếp trong đường tròn (O). Trên nửa mặt phẳng bờ AB không chứa M, vẽ tia Ax sao cho \(\widehat {xAB} = \widehat {AMB}\). Chứng tỏ Ax là tiếp tuyến của (O).
Hướng dẫn giải
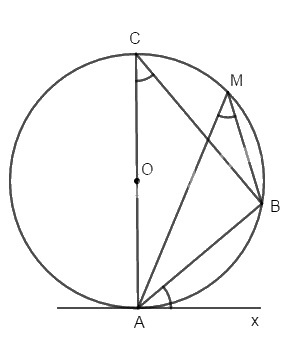
Vẽ đường kính AC của (O), ta phải chứng minh Ax vuông góc AC.
Thật vậy, ta có :
\(\widehat {ACB} = \widehat {AMB}\) (1)
( góc nội tiếp cùng chắn cung AB)
\(\widehat {AMB} = \widehat {xAB}\) (gt) (2)
mà \(\widehat {CBA} = 90^\circ \) ( AC là đường kính)
\(\Rightarrow \widehat {ACB} + \widehat {CAB} = 90^\circ \) (3)
Từ (1), (2) và (3) suy ra \(\widehat {CAB} + \widehat {xAB} = 90^\circ \)
Chứng tỏ Ax là tiếp tuyến của (O.
Xin các bạn lưu ý : Bài toán này là phần đảo của định lí về góc của tiếp tuyến và một dây, dùng để chứng minh.
Copyright © 2021 HOCTAP247
