Đề kiểm 15 phút - Đề số 2 - Bài 4 - Chương 3 - Hình học 9

Đề bài

Cho đường tròn (O; R). Từ điểm P ở bên ngoài đường tròn vẽ tiếp tuyến PT và cát tuyến PAB với (O).

Chứng minh rằng : \(PT^2 = PA.PB = PO^2- R^2\).

Hướng dẫn giải

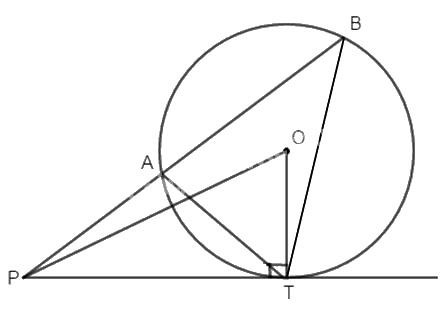
Ta có : \(\widehat {ABT} = \widehat {ATP}\) ( góc nội tiếp bằng góc giữa tiếp tuyến và một dây cùng chắn cung AT)

Do đó∆PAT và ∆PTB đồng dạng (g.g)

\(\Rightarrow \dfrac{{PA}}{{PT}} = \dfrac{{PT}}{{PB}} \Rightarrow P{T^2} = PA.PB\)

∆PTO vuông (PT là tiếp tuyến của (O))

Theo định lí Py-ta-go: \(P{T^2} = P{O^2}-O{T^2} = P{O^2} - {R^2}\).