Giải bài 32 trang 80 - Sách giáo khoa Toán 9 tập 2

Đề bài

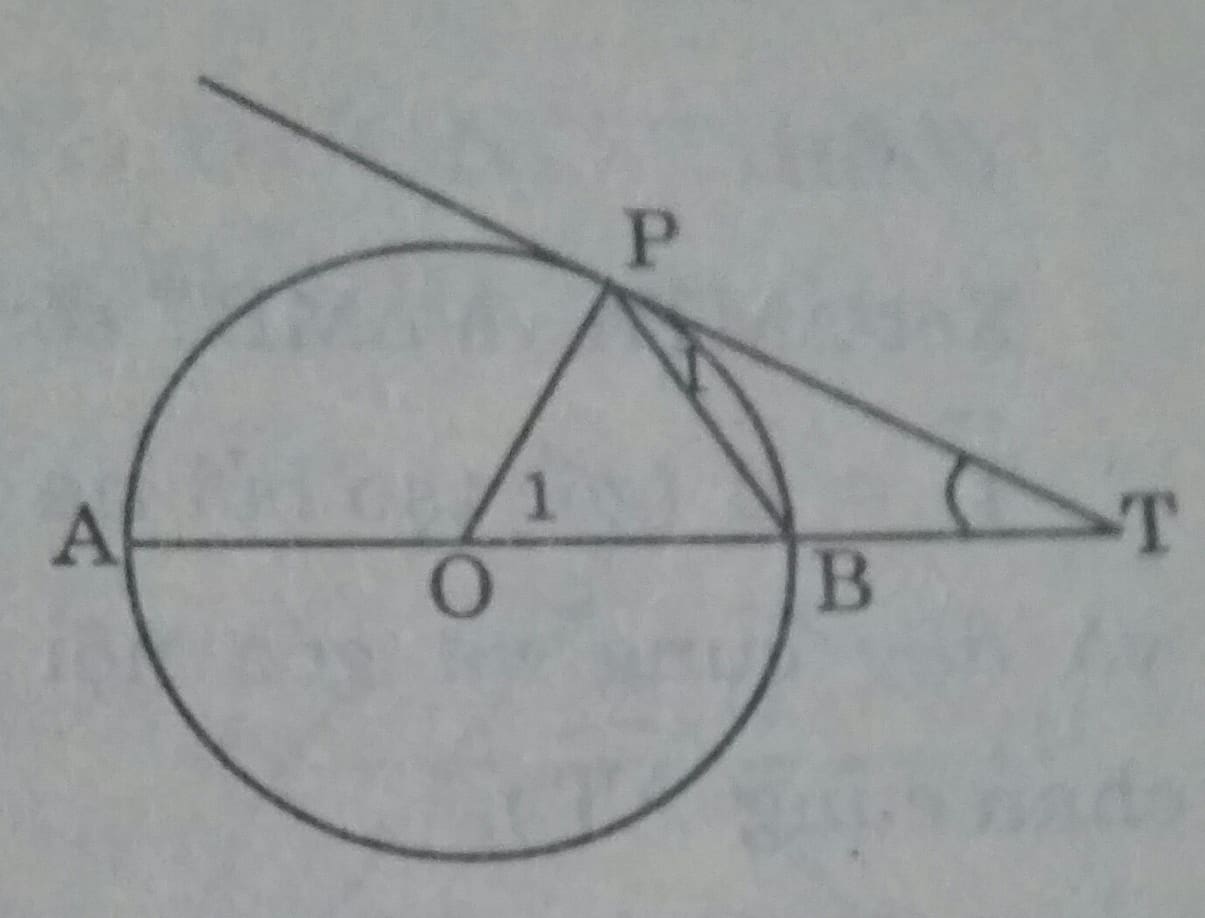
      Cho đường tròn tâm O đường kính AB. Một tiếp tuyến của đường tròn tại P cắt đường thẳng AB tại T (điểm B nằm giữa O và T).

Hướng dẫn giải

   Ta có

  \(\widehat{P_1}= \dfrac{1}{2} sđ\stackrel\frown{BP}; \widehat{O_1}= sđ\stackrel\frown{BP}\\ \Rightarrow \widehat{O_1}= 2\widehat{P_1}\\ Ta \ có \ OP \perp PT \Rightarrow \Delta POT \ vuông \ tại \ P\\ \Rightarrow \widehat{T }+ \widehat{O_1}= 90^0.\\ Vậy \ \widehat{BTP}+ 2.\widehat{TPB}= 90^0\)