Giải bài 30 trang 79 - Sách giáo khoa Toán 9 tập 2

Đề bài

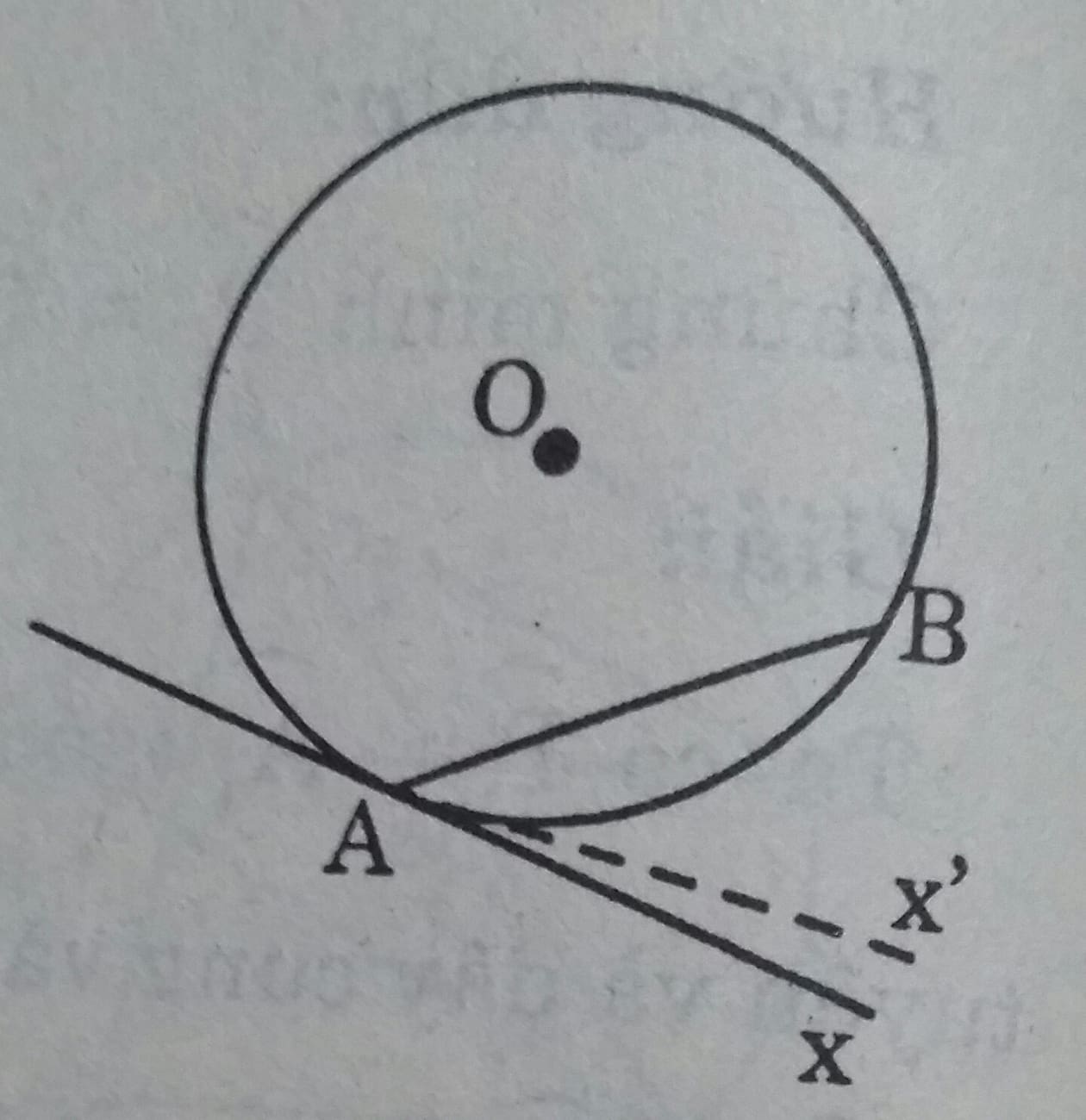
   Chứng minh định lí đảo của định lí về góc tạo bởi tia tiếp tuyến và dây cung , cụ thể là: Nếu góc BAx (với đỉnh A nằm trên đường tròn, một cạnh chứa dây cung AB), có số đo bằng nửa số đo của cung AB căng dây đó và cung này nằm bên trong góc đó thì cạnh Ax là một tia tiếp tuyến của đường tròn .

Hướng dẫn giải

  Trên nửa mặt phẳng bờ AB có chứa tia Ax ta vẽ tia Ax' là tia tiếp tuyến của đường tròn (O). Ta được:

   \(\widehat{BAx'}= \dfrac{1}{2}sđ \stackrel\frown{AB}\)

  \(\widehat{BAx }= \dfrac{1}{2}sđ \stackrel\frown{AB}\)(gt)

  Suy ra \(\widehat{BAx'}= \widehat{BAx } \Rightarrow\) hai tia Ax' và Ax trùng nhau.

  Vậy tia Ax là một tia tiếp tuyến của đường tròn.