Đề kiểm 15 phút - Đề số 4 - Bài 4 - Chương 3 - Hình học 9

Đề bài

Hai đường tròn (O) và (O’) cắt nhau tại A và B. Qua A vẽ tiếp tuyến AM với (O’) và tiếp tuyến AN với (O) (\(M \in (O), N \in (O’)\)). Chứng minh rằng: \(AB^2= MB.NB\) và \(\widehat {MBA} = \widehat {NBA}\).

Hướng dẫn giải

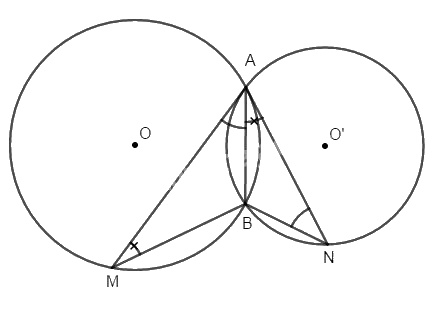
Hai tam giác ABM và NBA có :

+) \(\widehat {AMB} = \widehat {BAN}\)

+) \(\widehat {ANB} = \widehat {MAB}\) ( góc giữa tiếp tuyến và một dây bằng góc nội tiếp cùng chắn cung AB)

\(∆ABM\) đồng dạng \(∆NBA\) (g.g)

\(\Rightarrow\dfrac{{AB}}{{NB}} = \dfrac{{MB} }{ {AB}}\)

\(\Rightarrow AB^2= MB.NB\) và có \(\widehat {MBA} = \widehat {NBA}\).