Chuyên đề về giới hạn hàm số và xét tính liên tục của hàm số trên R

Chuyên đề về giới hạn hàm số và xét tính liên tục của hàm số trên R

Để đáp ứng nhu cầu học tập và rèn luyện tham khảo thêm chuyên đề giới hạn hàm số cho các em, cùng học vui xin giới thiệu một tài liệu rất thú vị về chương học mà được rất nhiều các bạn học sinh quan tâm. Bài viết chắc chắn sẽ đem lại cho bạn đọc những điều bổ ích. Hãy cùng chúng tôi khám phá nhé!

I. Định nghĩa

Giới hạn hàm số tại một điểm: Cho hàm số f(x) xác định trên tập  \(X\subset R\)và nhận giá trị trên R, \(x_0\) là một điểm giới hạn của tập X, hàm số đã cho là hàm số liên tục trên R.

Định nghĩa:

Số l  được gọi là giới hạn hàm số f(x) khi x dần tới \(x_0\) nếu \(\forall \varepsilon >0, \exists \delta>0\), sao cho \(\forall x: |x-x_0|<\delta\) thì \(|f(x)-l|<\varepsilon \Leftrightarrow \lim \limits_{x\to x_0} f(x)=l\)

Định lý:

• Nếu \(\lim \limits_{x\to x_0}f(x)=A\) thì A là duy nhất
• \(\lim \limits_{x\to x_0}f(x)=l \Leftrightarrow \lim \limits_{x\to x_0-0}f(x)=\lim \limits_{x\to x_0+0}f(x)=l\)
• \(\lim \limits_{x\to a}f(x)=l, a<f(x)<b \Leftrightarrow a\le l\le b\)

Điều kiện tồn tại giới hạn hàm số:

• Định lý 1: \(\lim \limits_{x\to x_0}f(x)=A\Leftrightarrow \forall {x_n}\subset X,\lim \limits_{n\to \infty}f(x_n)=A\)
• Định lý 2: f(x) xác định trên X khi đó:

\(\lim \limits_{x\to a}f(x)=l\Leftrightarrow \forall \varepsilon >0, \exists \delta >0 \forall x'.x'': 0<|x'-a|<\delta;0<|x''-a|<\delta \Rightarrow |f(x')-f(x'')|<\varepsilon\)

Luyện tập ngay tại: 

• Giới hạn hàm số
• Bài tập về hàm số liên tục

II. Hàm số liên tục

1. Định nghĩa

Định nghĩa 1: Hàm số f(x) xác định trong khoảng (a, b) và \(x_0\in (a;b)\). Hàm số đó được gọi là liên tục tại điểm \(x_o\) nếu: \(\lim\limits_{x \to x_o}f(x)=f(x_o)\).

Định nghĩa 2: Hàm số liên tục trên khoảng (a, b), nếu liên tục tại mọi điểm trên (a, b).

Định nghĩa 3: Xét tính liên tục của hàm số liên tục trong [a,b], liên tục trên khoảng (a,b) và liên tục phải tại a, liên tục trái tại b, hay \(\lim\limits_{x \to a+0}f(x)=f(a+0)\) hoặc \(\lim\limits_{x \to b-0}f(x)=f(b-0)\).

2. Tính liên tục của hàm số

• Định lý: Nếu hàm số f liên tục tại điển a và f(a) > 0 (hay f(a) < 0) thì tồn tại một lân cận của a để sao cho với mọi x thuộc lân cận đó thì f(x) > 0(hay f(x) < 0).
• Định lý Bônxanô-Côsi thứ nhất: Nếu f(x) xác định,liên tục trên [a,b]và f(a).f(b) < o. Khi đó \(\exists c\in (a,b):f(c)=C\).
• Định lý Bônxanô-Côsi thứ hai: Nếu f(x) xác định,liên tục trên [a,b]và f(a) = A, f(b) = B,thì \(\forall C:A<C<B\Rightarrow \exists\in(a;b):f(c)=C\).

3. Hàm số đồng biến

Điều kiện cần và đủ để y = f(x) đồng biến trên khoảng (a,b) \(↔ f’ (x) ≥ 0, ∀x ∈ (a,b)\) đồng thời \(f’ (x) =0\) chỉ xảy ra tại một số hữu hạn điểm thuộc (a,b).

Ví dụ: Cho hàm số \(y = {x^3} - 3(2m + 1){x^2} + (12m + 5)x + 2\)
Tìm m để hàm số đồng biến trên khoảng \((2; + ∞).\)

\([2; +∞) ↔ 0 ≤ y’, ∀x ∈ (2; +∞) ↔ 12m(x - 1) ≤ 3x2 - 6x + 5 ,∀x ∈ (2; +∞)\)
\(⇔\dfrac{x2−6x+5}{12(x−1)}≥m ∀x ∈ (2; +∞)\)
\(f’(x) = \dfrac{3x(x−2)+1}{12(x−1)^2} → f’(x) > 0, ∀x ∈ (2; +∞)\)
\(→ f(x)\) đồng biến trên \( (2; +∞)\) nên \(f(x)>f(2)=\dfrac{5}{12}⇔m≤\dfrac{5}{12}\)

4. Hàm số nghịch biến

Điều kiện cần và đủ để y = f(x) nghịch biến trên khoảng (a,b) \( ↔ f’ (x) ≤ 0, ∀x ∈ (a,b)\) đồng thời \( f’ (x) =0\) chỉ xảy ra tại một số hữu hạn điểm thuộc (a,b).

Ví dụ: Tìm m để hàm số \(y = \dfrac{{m{x^2} + 6x - 2}}{{x + 2}}\) nghịch biến trên \([1; + ∞).\)

Hàm nghịch biến trên
\([1; + ∞) ↔ y’ ≤ 0 ,∀x ∈ [1; + ∞)↔mx^2 + 4mx + 14 ≤0; ∀x ∈[1; + ∞)\)

\(\begin{array}{l} \Leftrightarrow \dfrac{{ - 14}}{{{x^2} + 4x}} \ge m\,\,\forall x \in (2; + \infty )\\ f'(x) = \dfrac{{12(2x + 4)}}{{{{(x + 2)}^2}}} > 0 \Rightarrow f'(x) > 0\,\forall x \in \left[ {1; + \infty } \right)\\ \end{array}\)

\(\to f(x\) đồng biến trên  \(\left[ {1; + \infty } \right)\) nên \(f(x) > f(1) = \frac{{ - 14}}{5} \Leftrightarrow m \le \frac{{ - 14}}{5} \).

Có thể bạn quan tâm: 

• Nguyên hàm
• Giới hạn
• Bộ công thức đạo hàm chuẩn, đầy đủ nhất dành cho các bạn học sinh THPT

III. Công thức tính giới hạn hàm số

1. Giới hạn hữu hạn

• Giới hạn đặc biệt

Cách tính lim đặc biệt như sau:

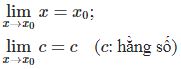
• Định lý

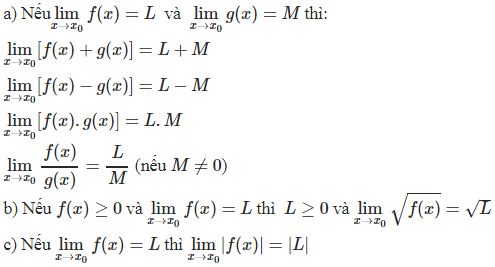
2. Giới hạn vô cực. Giới hạn ở vô cực

• Giới hạn đặc biệt

Cách tính giới hạn hàm số đặc biệt như sau:

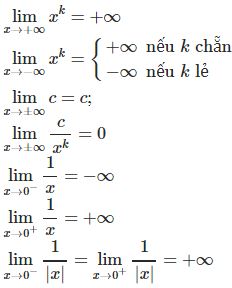
• Định lý

Trên đây là bản tổng hợp đầy đủ nhất về chương giới hạn, hy vọng nó giúp bạn hiểu rõ về các dạng kiến thức trong học phần này. Chúng tôi tin rằng chỉ cần có sự đầu tư thời gian thì chúng sẽ không thể làm khó được bạn. Chúc các bạn thành công!

Giới hạn

Các giới hạn hay gặp

Tổng hợp đầy đủ những công thức giới hạn học sinh không nên bỏ qua

Tổng hợp đầy đủ những giới hạn hay gặp mà học sinh không thể bỏ qua

Tổng hợp lý thuyết và bài tập đường tiệm cận của hàm số

• Giới hạn
• Các giới hạn hay gặp
• Tổng hợp đầy đủ những công thức giới hạn học sinh không nên bỏ qua
• Tổng hợp đầy đủ những giới hạn hay gặp mà học sinh không thể bỏ qua
• Tổng hợp lý thuyết và bài tập đường tiệm cận của hàm số