Diện tích hình vuông - Công thức toán học quan trọng không thể thiếu
Công thức : Diện tích hình vuông - Công thức toán học quan trọng không thể thiếu
Diện tích hình vuông - Công thức toán học quan trọng không thể thiếu
Cùng học vui giới thiệu bạn đọc về bộ lý thuyết và công thức tính diện tích hình vuông thuộc chương trình Toán lớp 8. Bài viết dưới đây là tổng hợp các lý thuyết về định nghĩa, đặc điểm và dấu hiệu nhận biết hình vuông cũng như công thức tính chu vi, diện tích và các bài tập liên quan. Hãy cùng chúng tôi tìm hiểu nhé!
I. Định nghĩa
1. Hình vuông là gì?
Hình vuông là hình tứ giác có 4 góc vuông và 4 cạnh bằng nhau.
Cũng có thể nói hình vuông là:
- Hình chữ nhật có các cạnh bằng nhau.
- Hình thoi có 2 đường chéo bằng nhau.
- Hình vuông vừa là hình chữ nhật vừa là hình thoi.
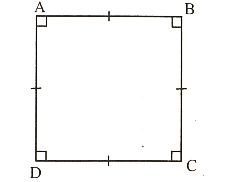
2. Tính chất hình vuông
- Hai đường chéo hình vuông bằng nhau, vuông góc và giao nhau tại trung điểm của mỗi đường.
- Giao điểm hai đường chéo của hình vuông là tâm của đường tròn nội tiếp và ngoại tiếp.
- Giao của các đường phân giác, trung tuyến, trung trực đều trùng tại một điểm.
- Một đường chéo sẽ chia hình vuông thành hai phần có diện tích bằng nhau.
- Có một đường tròn nội tiếp và ngoại tiếp, đồng thời tâm của cả hai đường tròn trùng nhau và là giao điểm của hai đường chéo của hình vuông.
- Hình vuông có tất cả tính chất của hình chữ nhật và hình thoi.
3. Dấu hiệu nhận biết hình vuông
- Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
- Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
- Hình chữ nhật có một đường chéo là đường phân giác một góc là hình vuông.
- Hình thoi có một góc vuông là hình vuông.
- Hình thoi có hai đường chéo bằng nhau là hình vuông.
Nhận xét: Một hình tứ giác vừa là hình chữ nhật, vừa là hình thoi thì đó là tứ giác vuông.
Có thể bạn quan tâm:
4. Các dạng toán liên quan
- Vận dụng dấu hiệu nhận biết đã cho để chứng minh tứ giác đó là hình vuông.
- Vận dụng kiến thức về hình vuông để chứng minh các dạng toán cơ bản: Chứng minh một tứ giác là hình vuông, tìm thêm điều kiện của đề bài để chứng minh một tứ giác là hình vuông, tính độ dài cạnh,...
II. Công thức tính chu vi hình vuông
1. Lý thuyết
Chu vi hình vuông bằng tổng độ dài 4 cạnh của nó, hay bằng 4 lần độ dài một cạnh:
\({\displaystyle P=a\times 4\,}\)
2. Bài tập
Câu 1:
Muốn tính chu vi hình vuông ta lấy:
A. Chiều dài cộng chiều rộng (cùng đơn vị đo) rồi nhân 2.
B. Độ dài một cạnh nhân với chính nó.
C. Độ dài một cạnh nhân 4.
Câu 2:
Điền số thích hợp vào chỗ chấm.
Chu vi hình vuông có cạnh bằng 9dm là .......... dm.
Câu 3:
Một hình vuông có chu vi của một hình chữ nhật có chiều dài 13cm, chiều rộng 5cm. Hỏi hình vuông đó có cạnh dài bao nhiêu xăng−ti−mét?
Trả lời:
Độ dài cạnh của hình vuông đó là: ............. cm.
Đáp án:
| 1 | 2 | 3 |
| C | 36 dm | 9dm |
Hot: Tổng hợp các Mẹo Toán học hữu ích nhất
III. Công thức tính diện tích hình vuông
1. Lý thuyết:
Cách tính diện tích hình vuông
Diện tích hình vuông bằng bình phương độ dài của cạnh:
\({\displaystyle S=a^{2}\,}\)
2. Bài tập
Câu 1: Tính diện tích của hình vuông có cạnh bằng 80m.
Trả lời:
Áp dụng công thức tính diện tích hình vuông ta có \(S = 80^2= 6400 (m^2)\)
Câu 2: Một hình vuông có chu vi 36cm. Tính diện tích hình vuông đó.
Trả lời:
Gọi a là cạnh của hình vuông.
Áp dụng công thức tính chu vi hình vuông ta có: \(a=\dfrac{36}{4}=9(cm)\)
Vậy diện tích của hình vuông là: \(S=9^2=81(cm^2)\).
Câu 3: Tìm diện tích của một hình vuông có chu vi bằng chu vi của hình chữ nhật có chiều dài 12 cm, chiều rộng 6 cm.
Trả lời: Từ giả thiết đã cho ta có chu vi hình vuông = chu vi hình chữ nhật = (12 + 6).2 = 36 (cm).
Gọi a là cạnh của hình vuông.
Áp dụng công thức tính chu vi hình vuông ta có: \(a=\dfrac{36}{4}=9(cm)\)
Vậy diện tích của hình vuông là: \(S=9^2=81(cm^2)\).
Luyện thêm tại:
Vừa rồi chúng tôi đã giúp bạn tổng hợp các kiến thức cơ bản về hình vuông và đưa ra các bài tập liên quan có lời giải. Mọi thắc mắc về bài học xin vui lòng để lại dưới mục bình luận, cảm ơn quý bạn đọc đã quan tâm đến bài viết của chúng tôi!
Công thức tính diện tích, chu vi và đường chéo hình vuông
Copyright © 2021 HOCTAP247
