Trọn bộ công thức tính diện tích tam giác thường gặp dành cho học sinh

Trọn bộ công thức tính diện tích tam giác thường gặp dành cho học sinh

Các bạn đang tìm kiếm cách tính diện tích tam giác chuẩn để giải các tập liên quan, vậy hãy cùng tham khảo bài viết dưới đây. Bài viết chia sẻ các công thức tính diện tích về tam giác thường, vuông, cân, đều và một số bài tập mẫu tham khảo. Hy vọng sẽ đem lại cho bạn bộ công thức chuẩn để áp dụng giải quyết các bài tập về hệ thức lượng trong tam giác.

I. Cách tính diện tích tam giác thường

Đinh nghĩa:

Tam giác thường là tam giác có độ dài các cạnh khác nhau, số đo góc trong khác nhau.

Phương pháp tính diện tích:

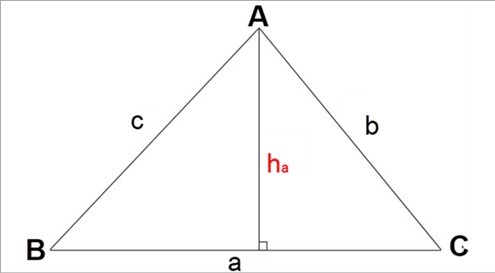
Các công thức tính diện tích tam giác thường:

Diện tích tam giác bằng ½ tích của chiều cao và chiều dài cạnh đáy tam giác:

\(S_{\Delta}ABC=\dfrac{1}{2}a.h_a=\dfrac{1}{2}b.h_b=\dfrac{1}{2}c.h_c\)

Diện tích tam giác bằng ½ tích hai cạnh và sin của góc hợp bởi hai cạnh đó trong tam giác:

\(S_{\Delta}ABC=\dfrac{1}{2}a.b.sinC=\dfrac{1}{2}a.c.sinB=\dfrac{1}{2}b.c.sinA\)

Sử dụng công thức Heron :

\(S=\sqrt{p(p−a)(p−b)(p−c)}\)

trong đó: \(p=\dfrac{1}{2}(a+b+c)\) là nửa chu vi của tam giác.

Với R là bán kính đường tròn ngoại tiếp tam giác, các bạn có công thức:

\(S_{\Delta}ABC=\dfrac{abc}{4R}\)

Với r là bán kính đường tròn nội tiếp tam giác, ta có:

\(S_{\Delta}ABC=p.r\)

Các bạn có thể sử dụng công thức tính diện tích tam giác:

\(S_{\Delta}ABC=2.R^2.sinA.sinB.sinC\)

II. Cách tính diện tích tam giác vuông

Tam giác vuống ABC có độ dài hai cạnh góc vuông lần lượt là a và b. Diện tích tam giác ABC là:

\(S_{\Delta}ABC=\dfrac{1}{2}a.b\)

III. Cách tính diện tích tam giác cân

Tam giác cân ABC, có độ dài cạnh đáy là a, độ dài hai cạnh bên là b, chiều cao là \(h_a\) hạ từ góc đỉnh xuống cạnh đáy:

Công thức tính diện tích: \(S_{\Delta}ABC=\dfrac{1}{2}a.h_a\)

IV. Cách tính diện tích tam giác đều cạnh a

Tam giác đều ABC có độ dài các cạnh bằng nhau và đều bằng a. Diện tích tam giác ABC là:

\(S_{\Delta}ABC=a^2\dfrac{\sqrt3}{4}\)

V. Một số bài tập mẫu và phương pháp giải

    1. Các dạng bài tập liên quan

Bài 1: Cho tam giác AOB vuông tại O với đường cao OM (h.131). Hãy giải thích vì sao ta có đẳng thức AB.OM = OA.OB

Đáp án: 

Ta có cách tính diện tích ΔAOB với đường cao OM và cạnh đáy AB:

 \(S=\dfrac{1}{2}OM.AB\)

Ta lại có cách tính diện tích ΔAOB vuông với hai cạnh góc vuông OA, OB là:

 \(S=\dfrac{1}{2}OA.OB\)

Suy ra AB.OM = OA.OB (vì cùng = 2S)

Bài 2: Cho tam giác ABC và đường trung tuyến AM. Chứng minh: SAMB = SAMC

Lời giải:

Kẻ đường cao AH.

Ta có: \(S_{AMB}=\dfrac{1}{2}.BM.AH\)

\(S_{AMC}=\dfrac{1}{2}.CM.AH\)

Mà BM = CM (vì AM là trung tuyến)

Vậy \(S_{AMB} = S_{AMC}\) (đpcm)

Bài 3: Tính diện tích của một tam giác biết 3 cạnh. Cho tam giác cân ABC có cạnh đáy BC = a và cạnh bên AB = AC = b.

Lời giải:

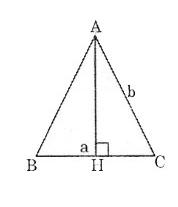
Gọi AH = h là chiều cao của tam giác cân.

Theo định lí Pitago ta có:

\(h^2=b^2-(\dfrac{a}{2})=\dfrac{4b^2-a^2}{4}\)

\(h=\dfrac{\sqrt{4b^2-a^2}}{2}\)

Nên \(S = \dfrac{1}{2}ah=\dfrac{1}{2}a.\dfrac{\sqrt{4b^2-a^2}}{4}=\dfrac{1}{4}a.\sqrt{4b^2-a^2}\)

Bài 4: Tính x sao cho diện tích hình chữ nhật ABCD gấp 3 lần diện tích \(ΔADE\)

Cách 1:

Áp dụng: công thức tính diện tích tam giác, diện tích hình chữ nhật, biểu diễn diện tích hình chữ nhật theo diện tích của \(ΔADE\).

Lời giải chi tiết

Ta có: AD = BC = 5cm (gỉa thuyết)

Diện tích  \(ΔADE\) là: \(S_{ADE}=\dfrac{EH.AD}{2}=\dfrac{2.5}{2}=5cm^2\)

Diện tích hình chữ nhật ABCD là: \(SABCD=5x(cm^2)\)

Theo đề bài ta có: 

\(S_{ABCD}=3S_{ADE}⇒5x=3.5=15⇒x=15:5=3cm\)

Vậy \( x=3cm\).

Cách 2:

Ta có AD = BC = 5cm

\(S_{ADE}=\dfrac{1}{2}2.5=5cm^2\)

Diện tích hình chữ nhật ABCD: \(S_{ABCD} = 5x\)

Theo đề bài ta có \(S_{ABCD} = 3S_{ADE}\) nên \( 5x = 3.5\)

Vậy \( x=3cm\)

    2. Một số tips làm bài tập liên quan đến tính diện tích tam giác

Dạng bài tập liên quan đến tính diện tích tam giác không phải là dạng bài tập khó. Tuy nhiên, các công thức này thường được sử dụng trong các bài tập tính toán tổng hợp rất nhiều, nên các bạn cần phải ghi nhớ các các công thức này một cách chính xác. Sau đây là một số cách tổng hợp được mà các học sinh thường sử dụng:

Học toán trên trường lớp

• Nắm chắc các lý thuyết, định nghĩa: Các tính chất, công thức, định nghĩa phải nhớ thì các em mới vận dụng nó vào bài tập để chứng minh, giải thích hay phân tích được. Xem thêm tạị Công thức tính diện tích tam giác, Tính diện tích tam giác theo tọa độ mặt phẳng, Công thức tính độ dài đường trung tuyến, công thức tính chu vi, diện tích tam giác,...
• Không học dồn: Đối với các môn tự nhiên như toán lý hóa, đặc biệt là môn Toán, thì các em phải học vững cái trước thì mới học tốt được cái sau. Việc học dồn là điều không thể để xảy ra với môn học này. Khi các em đã bỏ quá nhiều mà giờ phải học dồn sẽ không hiểu quả và ảnh hưởng đến sức khỏe của mình nữa.
• Lắng nghe và ghi chép mọi thông tin từ bài giảng: Đa số bài giảng của thầy cô đều nằm trong sách tới 80% và chỉ 20% là ở ngoài sách để các em hiểu sâu hơn. Vì thế, hãy ghi chép tất cả những gì thầy cô giảng dạy, nó sẽ rất hiệu quả đấy!
• Mạnh dạn hỏi khi chưa hiểu: Hãy mạnh dạn dơ tay để hỏi Thầy Cô của mình để họ giảng lại hay giải thích cho các bạn nghe nhé. Vì khi các em hiểu sâu, các em mới làm bài tập và khắc ghi trong đầu được, gạt bỏ được tâm lý ngại ngùng.

Tự học toán tại nhà

• Đọc trước bài mới ở nhà: Bổ sung thêm kiến thức môn Toán tại Công thức Toán học
• Học và làm bài tập thật nhiều: Tham khảo thêm: Các bài tập về diện tích tam giác

Trên đây là tổng hợp bộ công thức tính diện tích tam giác thuồng gặp trong chương trình học. Hy vọng nó sẽ trang bị cho bạn một lượng kiến thức cần thiết để giải quyết các vấn đề liên quan. Chúc các bạn thành công!

Công thức tính diện tích và chu vi hình tam giác

Công thức tính đường trung tuyến của hình tam giác

Công thức tính đường phân giác của hình tam giác

• Công thức tính đường phân giác của hình tam giác
• Công thức tính đường trung tuyến của hình tam giác
• Công thức tính diện tích và chu vi hình tam giác