Lý thuyết và bài tập áp dụng phương trình đường Hypebol

Lý thuyết và bài tập áp dụng phương trình đường Hypebol

Bài giảng “Phương trình hypebol” giúp các bạn tìm hiểu và giải bài toán liên quan đến hypebol trong hệ trục tọa độ Oxy. Chúng tôi gửi bản tổng hợp chi tiết đến các bạn!

I. Định nghĩa đường hypebol

Trong toán học, hyperbol hay hypecbol là một kiểu Đường cô-nic, được định nghĩa là đường giao của một mặt nón với một mặt phẳng cắt cả hai nửa của hình nón.

Đường hyperbol còn được định nghĩa là quỹ tích của những điểm trong mặt phẳng có giá trị tuyết đối của hiệu khoảng cách tới hai điểm cố định là một hằng số bằng 2a. a đồng thời cũng bằng độ dài bán trục lớn của Hyberbol. Hai điểm cố định đó gọi là hai tiêu điểm của hyperbol. Đường thẳng đi qua hai tiêu điểm này được gọi là trục thực của hyberbol và trung điểm của đoạn thẳng nối hai tiêu điểm này được gọi là tâm của hình hyperbol.

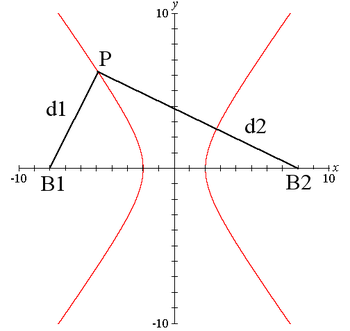
>>>Xem thêm tại: Các công thức Hypebol

II. Phương trình Hypebol

• Hình Hypebol: 

Hình Hyperbol nằm theo hướng Đông-Tây với tâm có tọa độ là (h,k):

\({\displaystyle {\frac {\left(x-h\right)^{2}}{a^{2}}}-{\frac {\left(y-k\right)^{2}}{b^{2}}}=1}\)

• Phương trình chính tắc của đường hyperbol trong hệ tọa độ Descartes khi có tâm trùng với gốc tọa độ:

\({\displaystyle {\frac {\left(x\right)^{2}}{a^{2}}}-{\frac {\left(y\right)^{2}}{b^{2}}}=1}\)

Trong đó:

- \( {\displaystyle c^{2}=a^{2}+b^{2}}\) và 2c là tiêu cự

- Tâm sai được tính bằng công thức:

\({\displaystyle \varepsilon ={\sqrt {1+{\frac {b^{2}}{a^{2}}}}}=\sec \left(\arctan \left({\frac {b}{a}}\right)\right)=\cos \left(\operatorname {arsin} \left({\frac {b}{a}}\right)\right)}\)

- Tiêu điểm của đường hypebol được xác định bởi công thức: \({\displaystyle \left(h\pm c,k\right)}\)

- Đường chuẩn được xác định bởi công thức: \({\displaystyle x=h\pm a\;\cos \left(\arctan \left({\frac {b}{a}}\right)\right)}\), \({\displaystyle y=k\pm a\;\cos \left(\arctan \left({\frac {b}{a}}\right)\right)}\)

>>> Mọi người cũng tìm kiếm: Các công thức liên quan đến Elip, Các công thức liên quan đến đường tròn.

III. Các bài tập áp dụng phương trình đường Hypebol

Dạng phương trình chính tắc của Hypebol

Phương pháp giải:

Gọi phương trình chính tắc hypebol là \(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\), a,b>0

Từ giả thiết của bài toán ta thiết lập các phương trình, hệ phương trình từ giả thiết của bài toán để tìm các đại lượng của bài toán để tìm các đại lượng a, b của hypebol từ đó viết được phương trình chính tắc của nó.

Ví dụ: Viết phương trình chính tắc của Hypebol (H) trong mỗi trường hợp sau:

(H) có một tiêu điểm tọa độ là (-4 ; 0) và độ dài trục ảo bằng \(\sqrt {28}\)?

Gọi phương trình chính tắc của (H) là: \(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\) với \(b^2=c^2-a^2\)

(H) có một tiêu điểm tọa độ là (-4 ; 0) suy ra c = 4; độ dài trục ảo bằng \(\sqrt {28}\) suy ra \(2b= \sqrt{28}\) \(\leftrightarrow b^2=7, a^2=c^2-b^2=9\)

Vậy phương trình (H) là \(\dfrac{x^2}{9}-\dfrac{y^2}{7}=1\)

>>>Xem thêm bài tập và lời giải:

• Bài 38 trang 109 SGK Hình học 10 Nâng cao
• Bài 39 trang 109 SGK Hình học 10 Nâng cao
• Bài 40 trang 109 SGK Hình học 10 Nâng cao

Trên đây là bản tổng hợp chi tiết về lý thuyết đường Hypebol và các bài tập tham khảo. Để học tập tốt dạng bài này các bạn nên đầu tư nhiều thời gian hơn trong việc luyện tập. Hy vọng rằng chúng sẽ giúp bạn đjat được kết quả cao trong học tập!

Phương trình phân giác

Các công thức liên quan đến đường tròn

Các công thức liên quan đến Elip

Các công thức Hypebol

Lý thuyết phương trình đường tròn trong mặt phẳng tọa độ

Dạng bài liên quan đến phương trình đường thẳng trong mặt phẳng tọa độ

• Tính diện tích tam giác theo tọa độ trong mặt phẳng
• Phương trình đường thẳng
• Góc giữa 2 đường thẳng
• Khoảng cách từ 1 điểm tới đường thẳng
• Phương trình phân giác
• Các công thức liên quan đến đường tròn
• Các công thức Hypebol
• Các công thức liên quan đến Elip
• Dạng bài liên quan đến phương trình đường thẳng trong mặt phẳng tọa độ
• Lý thuyết phương trình đường tròn trong mặt phẳng tọa độ