Hệ thức lượng trong tam giác và các bài tập liên quan - cunghocvui

Hệ thức lượng trong tam giác và các bài tập liên quan

Không giống như học phần những hệ thức lượng trong tam giác vuông mà các bạn đã làm quen tại lớp 9, phần các hệ thức lượng trong tam giác thường lớp 10 có phần đa dạng và phức tạp hợp. Sau đây, chúng tôi sẽ giúp các bạn tổng hợp những kiến thức khó nhằn này!

I. Định lý hàm sin

Định lý hàm sin phát biểu như sau: Trong tam giaisc ABC với BC = a, AC = b, AB = c và R là bán kính đường tròn ngoại tiếp tam giác. Ta có:

\(\dfrac{a}{sinA}=\dfrac{b}{sinB}=\dfrac{c}{sinC}=2R\)

Tham khảo: Định lý hàm sin

II. Định lý hàm cos

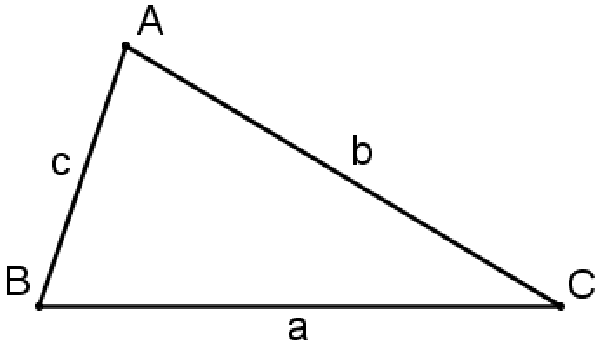
Định lý hàm cos phát biểu như sau: Trong một tam giác bất kỳ, bình phương một cạnh bằng tổng các bình phương của hai cạnh còn lại trừ đi hai lần tích cú hai cạnh đó nhân với cosin của góc xen giữa chúng.

Trong tam giác ABC vói BC = a, AC = b, Ab = c. Ta có:

\(a^2=b^2+c^2-2bc.cosA\\b^2=a^2+c^2-2ac.cosB\\a^2=b^2+a^2-2ba.cosc\)

Công thức hệ quả:

\(cosA=\dfrac{b^2+c^2-a^2}{2bc}\\cosB=\dfrac{c^2+a^2-b^2}{2ac}\\cosC=\dfrac{a^2+b^2-a^2}{2ab}\)

Tham khảo: Định lý hàm cosin

III. Độ dài đường trung tuyến

Cho tam giác ABC với \(m_1,m_2,m_3\) lần lượt là trung tuyến kẻ từ A, B, C. Ta có: 

\(m^2_a=\dfrac{2(b^2+c^2)-a^2}{4}\\m^2_b=\dfrac{2(a^2+c^2)-b^2}{4}\\m^2_c=\dfrac{2(b^2+a^2)-c^2}{4}\)

Xem ngay: Công thức tính độ dài trung tuyến trong tam giác

IV. Công thức tính diện tích tam giác

\(S=\dfrac{1}{2}ha_a=\dfrac{1}{2}absinC=pr=\dfrac{abc}{4R}=\sqrt{p-a)(p-b)(p-c)}\)

Với r là bán kình đường tròn nội tiếp tam giác ABC.

Xem ngay: Công thức tính diện tích tam giác

IV. Bài tập về hệ thức lượng trong tam giác lớp 10
Bài 1: Cho tam giác ABC có a = 12, b = 15, c = 13.

a) Tính số đo góc BAC?

b) Tính độ dài đường trung tuyến kẻ từ đỉnh C của tam giác?
c) Tính diện tích tam giác, bán kính đường tròn nội tiếp.
Bài 2: Cho tam giác ABC có AB = 6, AC = 8, góc \(\widehat{BAC} = 120^{\circ}\). Tính cạnh BC và bán kính đường tròn ngoại tiếp?

Bài 3: Cho tam giác ABC có \(\widehat{A}=60^{\circ},\widehat{B}=45^{\circ},b=2\) tính độ dài của cjanh a,c, bán kính đường tròn ngoại tiếp?

Bài 4: Cho tam giác ABC có \(m_b=4,m_c=2\)và a = 3 tính độ dài cạnh AB, AC.

Bài 5: Tính góc A của tam giác ABC có các cạnh a, b, c thỏa hệ thức \(b(b^2-a^2)=c(a^2-c^2)?\)

Bài 6: Cho tam giác ABC, chứng minh rằng: \(4(m_a^2+m_b^2+m_c^2)=3(a^2+b^2+c^2)\)

Bài 7: Cho tam giác ABC, chứng minh rằng: \(\dfrac{tan A}{tan B}=\dfrac{c^2+a^2-b^2}{c^2+b^2-a^2}\)

Bài 8: Cho tam giác ABC, chứng minh rằng: \(S=2R^2.sinA.sinB.sinC\)

Bài 9: Cho tam giác ABC, chứng minh rằng: \(c^2=(a-b)^2+4S(\dfrac{1-cosC}{sinC})\)

Bài 10: Cho tam giác ABC, chứng minh rằng: \(a=b.cosC+c.cosB\)

Tham khảo ngay: Các hệ thức lượng trong tam giác và giải tam giác

Mong rằng bài viết có thể giải đáp một phần các câu hỏi của các em như: hệ thức lượng trong tam giác là gì? quan hệ giữa ba cạnh và các góc của một tam giác là sao? Cánh chứng minh bằng hệ thức lượng trong tam giác. Cảm ơn các em đã xem bài viết này!

Định lí hàm số cosin

Định lí hàm số sin

Công thức tính độ dài trung tuyến trong tam giác

Công thức tính diện tích tam giác

• Định lí hàm số cosin
• Định lí hàm số sin
• Công thức tính độ dài trung tuyến trong tam giác
• Công thức tính diện tích tam giác