Trang chủ
Đề thi & kiểm tra
Vật lý
Đề minh họa tốt nghiệp THPT 2021 môn Lý có đáp án chi tiết từng câu
Một con lắc lò xo treo thẳng đứng, dao động...
Một con lắc lò xo treo thẳng đứng, dao động điều hòa tại nơi có g=10 m / s2.
Câu hỏi :
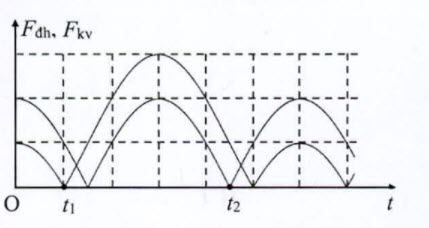
Một con lắc lò xo treo thẳng đứng, dao động điều hòa tại nơi có $g=10 {~m} / {s}^{2}$. Hinh bên là đồ thị biểu diễn sự phụ thuộc của độ lớn lực kéo về $F_{{kv}}$ tác dụng lên vật và độ lớn lực đàn hồi $F_{\text {db }}$ của lò xo theo thời gian $t$. Biết $t_{2}-t_{1}=\frac{7 \pi}{120}$ (s). Khi lò xo dãn $6,5 {~cm}$ thì tốc độ của vật là
A. 80{cm/s
B. 60 cm/s
C. 51 cm/s
D. 110 cm/s
* Đáp án
B
* Hướng dẫn giải
Có $F_{\mathrm{d} h} \max =k \cdot\left(\Delta l_{0}+A\right)>F_{k v} \max =k . A$$\rightarrow$ đường cao hơn là $\mathrm{F}_{{đh }}$, đường thấp hơn là $\mathrm{F}_{\mathrm{kv}}$.
Lập ti số: $\frac{F_{\text {dh }} m a x}{F_{k v} \max }=\frac{\Delta l_{0}+A}{A}=\frac{3}{2} \rightarrow \Delta l_{0}=\frac{A}{2}$
Tại $\mathrm{t}_{1}$ thì $\mathrm{F}_{\mathrm{d} \mathrm{h}}=0$ và $\mathrm{F}_{\mathrm{dl}}$ đang tăng
=> vật qua vị tri tự nhiên $\left(x=-\frac{A}{2}\right)$ theo chiều durơng Đến $\mathrm{t}_{2}$ thì $\mathrm{F}_{\mathrm{kv}}=0$ và $\mathrm{F}_{\mathrm{kv}}=0$ lần thứ $2 \mathrm{kề}$ tù $\mathrm{t}_{1} \rightarrow$ vật qua vị trí cân bằng theo chiều âm
$\rightarrow t_{2}-t_{1}=\frac{7 \pi}{120}=\frac{T}{12}+\frac{T}{2}=\frac{7 T}{12}=\frac{7 \pi}{120}(\mathrm{~s})$
$\rightarrow \mathrm{T}=0,1 \pi(\mathrm{s}) \rightarrow \omega=\frac{2 \pi}{T}=20(\mathrm{rad} / \mathrm{s})$
Có $ \Delta l_{0}=\frac{g}{\omega^{2}}=\frac{10}{20^{2}}=0,025(\mathrm{~m})=2,5 \mathrm{~cm} $
$\rightarrow \mathrm{A}=2 \Delta l_{0}=5(\mathrm{~cm})$ vị trí lò xo dãn } $6,5 \mathrm{~cm}$ có li độ $\mathrm{x}=6,5-2,5=4(\mathrm{~cm}) $
=> tốc độ $\mathrm{v}=\omega \sqrt{A^{2}-x^{2}}=20 \cdot \sqrt{5^{2}-4^{2}}=60(\mathrm{~cm} / \mathrm{s})$
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề minh họa tốt nghiệp THPT 2021 môn Lý có đáp án chi tiết từng câu
Số câu hỏi: 40
Copyright © 2021 HOCTAP247
