Trên mặt nước, phương trình sóng tại hai nguồn A, B ( Ab =20 cm ) đều có dạng:

Đáp án C

Phương pháp giải:

Bước sóng: $\lambda =vT=v.\frac{2\pi }{\omega }$

Số cực đại trên AB bằng số giá trị k nguyên thoả mãn: $-\frac{AB}{\lambda }<k<\frac{AB}{\lambda }$

Diện tích hình chữ nhật $ABCD$: $S=AB.BC\Rightarrow S_{\min }\iff B{C}_{\min }$

Giải chi tiết:

Bước sóng: $\lambda =vT=v.\frac{2\pi }{\omega }=60.\frac{2\pi }{40\pi }=3\left(cm\right)$

Số cực đại trên $AB$ bằng số giá trị $k$ nguyên thoả mãn:

$-\frac{AB}{\lambda }<k<\frac{AB}{\lambda }\iff -\frac{20}{3}<k<\frac{20}{3}\iff -6,7<k<6,7$

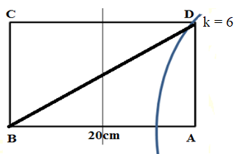
Diện tích hình chữ nhật $ABCD$:

$S=AB.BC\Rightarrow S_{\min }\iff B{C}_{\min }\iff k$ thuộc cực đại ứng với $k=6$

$\Rightarrow DB-DA=6.\lambda =6.3=18\left(cm\right)\left(1\right)$

Áp dụng định lí Pitago ta có:

$B{D}^2-D{A}^2=A{B}^2={20}^2$

$\Rightarrow \left(BD-DA\right)\left(BD+DA\right)={20}^2$

$\Rightarrow BD+DA=\frac{200}{9}\left(cm\right)\left(2\right)$

Giải hệ phương trình gồm hai phương trình (1) và (2) ta có: $\left\{\begin{array}{l}BD=20,11\left(cm\right)\\ DA=2,11\left(cm\right)\end{array}\right.$

Vậy diện tích nhỏ nhất của hình chữ nhật $ABCD$ là: $S=AB.BC=20.2,11=42,2\left(c{m}^2\right)$