Cho đoạn mạch xoay chiều AB nối tiếp gồm: AM chứa biến trở R, đoạn mạch MN chứa r, đoạn NP chứa cuộn cảm thuần

* Hướng dẫn giải

Đáp án A

Phương pháp giải:

Điện áp hiệu dụng: $U=I.Z$

Sử dụng giản đồ vecto

Bất đẳng thức Cô – si: $a+b\ge 2\sqrt{ab}$  (dấu “=” xảy ra $\iff a=b$

Giải chi tiết:

Điện áp hiệu dụng giữa hai đầu đoạn mạch AP là: 

$U_{AP}=\frac{U\sqrt{{\left(R+r\right)}^2+{Z_L}^2}}{\sqrt{{\left(R+r\right)}^2+{\left(Z_L-Z_C\right)}^2}}$

Để điện áp hiệu dụng giữa hai đầu đoạn mạch AP không phụ thuộc vào R, ta có: 

${\left(R+r\right)}^2+{Z_L}^2={\left(R+r\right)}^2+{\left(Z_L-Z_C\right)}^2$

$\Rightarrow {Z_L}^2={\left(Z_L-Z_C\right)}^2\Rightarrow Z_L=Z_C-Z_L\Rightarrow Z_C=2Z_L$

Ta có giản đồ vecto:

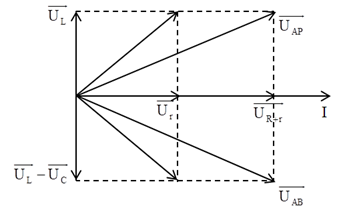
Từ giản đồ vecto, ta thấy góc lệch giữa $u_{AP}$  và $u_{AB}$  là:

 $\tan \left(2\alpha \right)=\frac{2\tan \alpha }{1-{\tan }^2\alpha }=\frac{2.\frac{Z_L}{R+r}}{1-{\left(\frac{Z_L}{R+r}\right)}^2}$ 

${\left(\tan 2\alpha \right)}_{\max }\Rightarrow {\left(2\alpha \right)}_{\max }\Rightarrow {\alpha }_{\max }\Rightarrow {\left(\tan \alpha \right)}_{\max }$ 

$\Rightarrow {\left(\frac{Z_L}{R+r}\right)}_{\max }\Rightarrow {\left(R+r\right)}_{\min }\Rightarrow R=0$

Khi đó ta có: 

$U_1=U_{BP}=U_C=\frac{U.Z_C}{\sqrt{r^2+{\left(Z_L-Z_C\right)}^2}}=\frac{U.2Z_L}{\sqrt{r^2+{Z_L}^2}}$

Ta có tích 

$U_{AN}.U_{NP}=\frac{U.\left(R+r\right)}{\sqrt{{\left(R+r\right)}^2+{\left(Z_L-Z_C\right)}^2}}.\frac{U.Z_L}{\sqrt{{\left(R+r\right)}^2+{\left(Z_L-Z_C\right)}^2}}$

$=U^2.\frac{Z_L.\left(R+r\right)}{{\left(R+r\right)}^2+{\left(Z_L-Z_C\right)}^2}=U^2.Z_L.\frac{1}{\left(R+r\right)+\frac{{\left(Z_L-Z_C\right)}^2}{R+r}}$

Đặt $x=R+r;f\left(x\right)=x+\frac{{\left(Z_L-Z_C\right)}^2}{x}\Rightarrow U_{AN}.U_{NP}=U^2.Z_L.\frac{1}{f\left(x\right)}$

Để tích ${\left(U_{AN}.U_{NP}\right)}_{\max }\Rightarrow f{\left(x\right)}_{\min }$

Áp dụng bất đẳng thức Cô – si, ta có: 

$x+\frac{{\left(Z_L-Z_C\right)}^2}{x}\ge 2\sqrt{x.\frac{{\left(Z_L-Z_C\right)}^2}{x}}=2\left|Z_L-Z_C\right|$

$f{\left(x\right)}_{\min }\iff x=\frac{{\left(Z_L-Z_C\right)}^2}{x}$

$\Rightarrow x^2={\left(R+r\right)}^2={\left(Z_L-Z_C\right)}^2={Z_L}^2$

$\Rightarrow R=Z_L-r$

Khi đó ta có: $U_2=U_{AM}=U_R=\frac{U.R}{\sqrt{{\left(R+r\right)}^2+{\left(Z_L-Z_C\right)}^2}}$

$\Rightarrow U_2=\frac{U.\left(Z_L-r\right)}{\sqrt{2{Z_L}^2}}=\frac{U.\left(Z_L-r\right)}{\sqrt{2}{Z}_L}$

Theo đề bài ta có:

$U_1=2.\left(\sqrt{6}+\sqrt{3}\right)U_2$

$\Rightarrow \frac{U.2Z_L}{\sqrt{r^2+{Z_L}^2}}=2.\left(\sqrt{6}+\sqrt{3}\right).\frac{U.\left(Z_L-r\right)}{\sqrt{2}{Z}_L}$

$\Rightarrow \sqrt{2}{Z_L}^2=\left(\sqrt{6}+\sqrt{3}\right).\left(Z_L-r\right).\sqrt{r^2+{Z_L}^2}$

$\Rightarrow {Z_L}^2=\frac{\sqrt{6}+\sqrt{3}}{\sqrt{2}}.\left(Z_L-r\right).\sqrt{r^2+{Z_L}^2}$

$\Rightarrow {\left(\frac{Z_L}{r}\right)}^2=\frac{\sqrt{6}-\sqrt{3}}{\sqrt{2}}.\left(\frac{Z_L}{r}-1\right).\sqrt{1+\frac{{Z_L}^2}{r^2}}\left(1\right)$

Đặt $\tan \alpha =\frac{Z_L}{r}$ , thay vào phương trình (1), ta có:

$x^2=\frac{\sqrt{6}+\sqrt{3}}{\sqrt{2}}\left(x-1\right)\sqrt{1+x^2}\Rightarrow x=\tan \alpha \approx 1.377$$\Rightarrow \alpha \approx {54}^0\Rightarrow 2\alpha ={108}^0$

Góc ${108}^0$  có giá trị gần nhất với góc $\frac{4\pi }{7}$