Ở mặt nước, một nguồn sóng đặt tại điểm O dao động điều hòa theo phương thẳng đứng. Sóng truyền trên mặt nước

Đáp án D

Phương pháp giải:

Độ lệch pha: $\Delta \phi =\frac{2\pi d}{\lambda }$

Công thức lượng giác: $\tan \left(a-b\right)=\frac{\tan a-\tan b}{1+\tan a\tan b}$

Hàm số $f\left(x\right)$ đạt cực trị khi  $f^{\text{'}}\left(x\right)=0$

Hệ thức lượng trong tam giác vuông: $\frac{1}{h^2}=\frac{1}{b^2}+\frac{1}{c^2}$

Giải chi tiết:

Điểm P dao động ngược pha với nguồn, giữa OP có 4 điểm ngược pha với O, ta có:

$\begin{array}{l}\Delta {\phi }_P=\frac{2\pi .OP}{\lambda }=\left(2k+1\right)\pi ;k=4\\ \Rightarrow OP=4,5\lambda \end{array}$

Điểm P dao động cùng pha với nguồn, giữa OQ có 8 điểm ngược pha với nguồn $\to k=8$

$\Delta {\phi }_Q=\frac{2\pi .OQ}{\lambda }=8.2\pi \Rightarrow OQ=8\lambda$

Ta có hình vẽ:

 

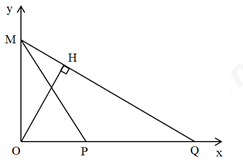
Ta có: $\widehat{PMQ}=\widehat{OMQ}-\widehat{OMP}\Rightarrow \tan \widehat{PMQ}=\tan \left(\widehat{OMQ}-\widehat{OMP}\right)$

$\Rightarrow \tan \widehat{PMQ}=\frac{\tan \widehat{OMQ}-\tan \widehat{OMP}}{1+\tan \widehat{OMQ}.\tan \widehat{OMP}}$

$\Rightarrow \tan \widehat{PMQ}=\frac{\frac{OQ}{OM}-\frac{OP}{OM}}{1+\frac{OQ}{OM}.\frac{OP}{OM}}=\frac{OM.\left(OQ-OP\right)}{O{M}^2+OQ.OP}=\frac{OM.PQ}{O{M}^2+OP.OQ}$

Đặt $OM=x\Rightarrow f\left(x\right)=\frac{x.PQ}{x^2+OP.OQ}$

Xét $f^{\text{'}}\left(x\right)=\frac{PQ.\left(x^2+OP.OQ\right)-2x.x.PQ}{{\left(x^2-OP.OQ\right)}^2}=\frac{-x^2.PQ+PQ.OP.OQ}{{\left(x^2-OP.OQ\right)}^2}$

Để $f{\left(x\right)}_{\max }\Rightarrow f^{\text{'}}\left(x\right)=0\Rightarrow -x^2.PQ+PQ.OP.OQ=0$

$\Rightarrow x=\sqrt{OP.OQ}=6\lambda$

Kẻ  $OH\perp MQ$

Áp dụng hệ thức lượng cho tam giác vuông OMQ , ta có:

$\frac{1}{O{H}^2}=\frac{1}{O{M}^2}+\frac{1}{O{Q}^2}\Rightarrow \frac{1}{O{H}^2}=\frac{1}{{\left(6\lambda \right)}^2}+\frac{1}{{\left(8\lambda \right)}^2}\Rightarrow OH=4,8\lambda$

Số điểm dao động ngược pha với O trên đoạn MH thỏa mãn:

$OH\le \left(2k+1\right)\lambda \le OM\Rightarrow 4,8\lambda \le \left(2k+1\right)\lambda \le 6\lambda$$\Rightarrow 1,9\le k\le 2,5\Rightarrow k=2$

→ trên MH có 1 điểm dao động ngược pha với nguồn

Số điểm dao động ngược pha với O trên đoạn QH thỏa mãn:

$OH\le \left(2k+1\right)\lambda \le OQ\Rightarrow 4,8\lambda \le \left(2k+1\right)\lambda \le 8\lambda$$\Rightarrow 1,9\le k\le 3,5\Rightarrow k=1;2;3$

→ trên QH có 3 điểm dao động ngược pha với nguồn

→ Trên MQ có 4 điểm dao động ngược pha với nguồn