Trên một sợi dây OB căng ngang, hai đầu cố định, đang có sóng dừng với tần số f xác định

* Hướng dẫn giải

Phương pháp:

Sử dụng kĩ năng đọc đồ thị 

Biên độ dao động của điểm cách nút sóng gần nhất một đoạn d là: $\text{A}=\text{A}\sin \frac{2\pi \text{d}}{\lambda }$ 

Hai điểm thuộc cùng bó sóng thì cùng pha với nhau

Hai điểm thuộc hai bó sóng liên tiếp thì ngược pha với nhau

Công thức độc lập với thời gian: $\frac{x^2}{A^2}+\frac{v^2}{{\omega }^2{A}^2}=1$ 

Sử dụng VTLG

Cách giải: 

Từ đồ thị ta thấy bước sóng:  = 24 (cm)

Gọi A là biên độ tại bụng, biên độ dao động của các điểm M, N, P là: 

$\left\{\begin{array}{l}{\text{A}}_{\text{M}}=\text{A}\left|\sin \frac{2\pi .\text{MB}}{\lambda }\right|=\text{A}\left|\sin \frac{2\pi .4}{24}\right|=\frac{\text{A}\sqrt{3}}{2}\\ {\text{A}}_{\text{N}}=\text{A}\left|\sin \frac{2\pi .\text{NB}}{\lambda }\right|=\text{A}\left|\sin \frac{2\pi .6}{24}\right|=\text{A}\\ {\text{A}}_{\text{P}}=\text{A}\left|\sin \frac{2\pi .38}{\lambda }\right|=\text{A.}\left|\sin \frac{2\pi \cdot 38}{24}\right|=\frac{\text{A}}{2}\end{array}\right.$ (*)

Ta thấy M, N thuộc cùng bó sóng, điểm P thuộc bó sóng liền kề

→ Hai điểm M, N cùng pha với nhau và ngược pha với điểm P 

Ta có: $\left\{\begin{array}{l}\frac{{\text{u}}_{\text{M}}}{{\text{u}}_{\text{N}}}=\frac{{\text{A}}_{\text{M}}}{{\text{A}}_{\text{N}}}=\frac{\frac{\text{A}\sqrt{3}}{2}}{ \text{A}}=\frac{\sqrt{3}}{2}\\ \frac{{\text{u}}_{\text{P}}}{{\text{u}}_{\text{M}}}=-\frac{{\text{A}}_{\text{P}}}{{\text{A}}_{\text{M}}}=\frac{\frac{\text{A}}{2}}{\frac{\text{A}\sqrt{3}}{2}}=\frac{1}{\sqrt{3}}\end{array}\right.$  

Tại thời điểm t1 có: ${\text{u}}_{\text{N}}={\text{A}}_{\text{M}}\Rightarrow {\text{u}}_{\text{M}}={\text{u}}_{\text{N}}\frac{\sqrt{3}}{\sqrt{2}}={\text{A}}_{\text{M}}\frac{\sqrt{3}}{2}$ 

Áp dụng công thức độc lập với thời gian, ta có: 

$\frac{{\text{u}}_{\text{M}}^2}{ {\text{A}}_{\text{M}}^2}+\frac{{\text{v}}_{\text{M}}^2}{{\omega }^2 {\text{A}}_{\text{M}}^2}=1\Rightarrow \frac{3}{4}+\frac{{60}^2}{{\omega }^2 {\text{A}}_{\text{M}}^2}=1$ 

$\Rightarrow \omega {\text{A}}_{\text{M}}=\omega \frac{\text{A}\sqrt{3}}{2}=120( \text{cm}/\text{s})\Rightarrow \omega \text{A}=80\sqrt{3}( \text{cm}/\text{s})$ 

Từ thời điểm t1 đến thời điểm t2, vecto quay được góc: $\Delta \phi =\omega \Delta \text{t}=2\pi \text{f.}\frac{11}{12\text{f}}=\frac{11\pi }{6}$ (rad)

Ta có VTLG: 

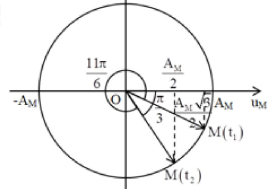
Từ VTLG, ta thấy ở thời điểm t2, điểm M có pha dao động là: $-\frac{\pi }{3}$ (rad) 

 Pha dao động của điểm P ở thời điểm t2 là: ${\phi }_{\text{p}}=-\frac{\pi }{3}+\pi =\frac{2\pi }{3}\left(\text{rad}\right)$ 

Vận tốc của điểm P ở thời điểm t2 là: 

${\text{v}}_P=-\omega {\text{A}}_P\sin {\phi }_P=-\frac{1}{2}\omega \text{A}\cdot \sin \frac{2\pi }{3}\Rightarrow {\text{v}}_P=-\frac{1}{2}.80\sqrt{3}.\frac{\sqrt{3}}{2}=-60( \text{cm}/\text{s})$ 

Chọn A.