Trang chủ
Đề thi & kiểm tra
Vật lý
[Năm 2022] Đề thi thử môn Vật lí THPT Quốc gia có lời giải (30 đề) !!
Ở mặt chất lỏng, tại hai điểm A và B...
Ở mặt chất lỏng, tại hai điểm A và B có hai nguồn dao động cùng pha theo phương thẳng đứng
Câu hỏi :
Ở mặt chất lỏng, tại hai điểm A và B có hai nguồn dao động cùng pha theo phương thẳng đứng phát ra sóng kết hợp với bước sóng . Gọi C và D là hai điểm trên mặt chất lỏng sao cho ABCD là hình vuông, I là trung điểm của AB, M là một điểm trong hình vuông ABCD xa nhất mà phần tử chất lỏng tại đó dao động với biên độ cực đại và cùng pha với nguồn. Biết AB = 6,6 . Độ dài đoạn thẳng MI gần nhất giá trị nào sau sau đây?
A. 100 N/ m.
B. 200 N/m.
C. 300 N/m.
D. 400 N/ m.
* Đáp án
A
* Hướng dẫn giải
Phương pháp:
Điều kiện có cực đại giao thoa trong giao thoa sóng hai nguồn cùng pha:
MI là đường trung tuyến của ∆MAB:
Sử dụng định lí Pitago trong tam giác vuông và các lí định lí liên quan đến tam giác.
Cách giải:
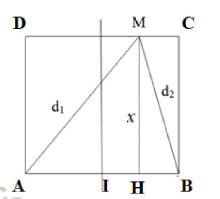
Áp dụng định lí Pitago ta có:
Cho
M dao động với biên độ cực đại và cùng pha với nguồn nên: ; Với
CI là đường trung tuyến của ∆CAB nên:
MI là đường trung tuyến của ∆MAB nên:
M là 1 điểm nằm trong hình vuông ABCD nên:
+
(1)
+
Lại có: AB = AH + HB
Đặt (3)
Xét các cặp k1, k2 thỏa mãn (1) (2) (3) ta tìm được:
Chọn A.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
[Năm 2022] Đề thi thử môn Vật lí THPT Quốc gia có lời giải (30 đề) !!
Số câu hỏi: 783
Copyright © 2021 HOCTAP247
