Đặt điện áp xoay chiều u = 120√2cos100πt (V) lên hai đầu đoạn mạch gồm cuộn dây

* Hướng dẫn giải

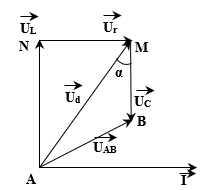
Ta có giản đồ vecto như hình vẽ.
Áp dụng định lí hàm số cosin cho ΔAMB được ${U^2} = U_d^2 + U_C^2 - 2{U_d}{U_C}\cos \alpha $.
→ $\cos \alpha = \frac{{U_d^2 + U_C^2 - {U^2}}}{{2{U_d}{U_C}}} = \frac{{{{160}^2} + {{56}^2} - {{120}^2}}}{{2.160.56}} = 0,8$
Trong ΔAMN có $\tan \alpha = \frac{{{U_r}}}{{{U_L}}} = \frac{{I.r}}{{I.{Z_L}}} = \frac{r}{{{Z_L}}}$
→ $r = {Z_L}.\tan \alpha = \omega L.\frac{{\sin \alpha }}{{\cos \alpha }} = \omega L\frac{{\sqrt {1 - {{\cos }^2}\alpha } }}{{\cos \alpha }} = 23,5\Omega .$