Người ta dùng hạt proton bắn vào hạt nhân _37Liđứng yên, để gây ra phản ứng _11p

* Hướng dẫn giải

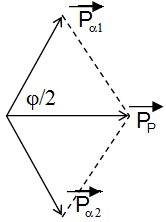
Theo ĐL bảo toàn động lượng ta có $\overrightarrow {{p_P}} = 2\overrightarrow {{p_\alpha }} $, với ${p^2} = 2mK$
$c{\rm{os}}\frac{\varphi }{2} = \frac{1}{2}\frac{{{p_P}}}{{{p_\alpha }}} = \frac{1}{2}\sqrt {\frac{{2{m_P}{K_P}}}{{2{m_\alpha }{K_\alpha }}}} = \frac{1}{2}\sqrt {\frac{{1.{K_P}}}{{4.{K_\alpha }}}} = \frac{1}{4}\sqrt {\frac{{{K_P}}}{{{K_\alpha }}}} $
Theo ĐL bảo toàn năng lượng toàn phần ta lại có.
$\Delta E + {K_P} = 2{K_\alpha } \Rightarrow \Delta E = 2{K_\alpha } - {K_P} > 0 \Rightarrow \frac{{{K_P}}}{{{K_\alpha }}} Từ đó suy ra $c{\rm{os}}\frac{\varphi }{2} 69,{3^0} \Leftrightarrow \varphi > 138,{6^0}$ (do hàm cosin nghịch biến)
→ góc có thể ${140^0}$.