Trang chủ
Đề thi & kiểm tra
Vật lý
Đề ôn luyện thi THPT Quốc gia môn Lý số 2 có đáp án
Trong thí nghiệm giao thoa trên mặt nước, hai nguồn...
Trong thí nghiệm giao thoa trên mặt nước, hai nguồn sóng kết hợp A và B dao động
Câu hỏi :
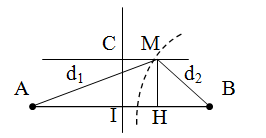
Trong thí nghiệm giao thoa trên mặt nước, hai nguồn sóng kết hợp A và B dao động cùng pha, cùng tần số, cách nhau AB = 8 cm tạo ra hai sóng kết hợp có bước sóng 2 cm. Đường thẳng Δ song song với AB và cách AB một khoảng 2 cm cắt đường trung trực của AB tại C, cắt vân giao thoa cực tiểu gần C nhất tại M. Khoảng cách CM là
A. 0,5 cm
B. 0,64 cm
C. 0,56 cm
D. 0,42 cm
* Đáp án
C
* Hướng dẫn giải
Gọi CM = IH = xTrên hình ta có. ${d_1} = \sqrt {A{H^2} + M{H^2}} = \sqrt {{{\left( {4 + x} \right)}^2} + {2^2}} $ (1)
${d_2} = \sqrt {B{H^2} + M{H^2}} = \sqrt {{{\left( {4 - x} \right)}^2} + {2^2}} $ (2)
Vì M cực tiểu nên có. ${d_1} - {d_2} = \left( {k + \frac{1}{2}} \right)\lambda $. Vì cực tiểu gần C nhất nên là cực tiểu thứ nhất, nhận k = 0.
Vậy có. ${d_1} - {d_2} = 1cm$(3).
Thay (1),(2) vào (3) → $\sqrt {{{\left( {4 + x} \right)}^2} + {2^2}} - \sqrt {{{\left( {4 - x} \right)}^2} + {2^2}} = 1$.
Giải phương trình ta được CM = x = 0,56cm.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề ôn luyện thi THPT Quốc gia môn Lý số 2 có đáp án
Số câu hỏi: 40
Copyright © 2021 HOCTAP247
