Trang chủ
Đề thi & kiểm tra
Vật lý
Đề ôn luyện thi THPT Quốc gia môn Lý số 4 có đáp án
Đặt điện áp xoay chiều u = U_0cos(ωt) vào hai...
Đặt điện áp xoay chiều u = U_0cos(ωt) vào hai đầu đoạn mạch AB có điện trở R =
Câu hỏi :
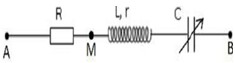
Đặt điện áp xoay chiều u = ${U_0}$cos(ωt) vào hai đầu đoạn mạch AB có điện trở R = 90 Ω mắc nối tiếp với cuộn dây không thuần cảm có r = 10 Ω và tụ điện có điện dung C thay đổi được theo thứ tự như hình vẽ.
M là điểm nối giữa R và cuộn dây, khi C = C1 thì điện áp hiệu dụng hai đầu đoạn mạch MB đạt giá trị cực tiểu bằng U1; Khi C = C2 = 0,5C1 thì điện áp hiệu dụng trên tụ điện đạt giá trị cực đại bằng U2. Tỉ số ${\frac{U_2}{U_1}}$ bằng
A. 2
B. 10
C. 52
D. 102
* Đáp án
D
* Hướng dẫn giải
+ Khi $C = {C_1}$Ta có ${U_{MB}} = \frac{{U\sqrt {{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}{{\sqrt {{R^2} + 2rR + {r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \frac{U}{{\sqrt {1 + \frac{{{R^2} + 2rR}}{{{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}} }}$
→ ${U_{MB\min }} \leftrightarrow {Z_L} = {Z_C}$ → cộng hưởng.
→ ${U_1} = {U_{MB\min }} = \frac{U}{{\sqrt {1 + \frac{{{R^2} + 2rR}}{{{r^2}}}} }} = \frac{U}{{10}}$ (*)
+ Khi $C = {C_2} = \frac{{{C_1}}}{2} \to {Z_{C2}} = 2{Z_{C1}} = 2{Z_L}$ (1)
${U_{C\max }} \to {Z_{C2}} = \frac{{{{\left( {R + r} \right)}^2} + Z_L^2}}{{{Z_L}}}$(2)
Từ (1)(2) → $Z_L^2 = {\left( {R + r} \right)^2} \to {Z_L} = 100\Omega .$.
${U_2} = {U_{C\max }} = \frac{{U\sqrt {{{\left( {R + r} \right)}^2} + Z_L^2} }}{{R + r}} = \frac{{U\sqrt {{{\left( {90 + 10} \right)}^2} + {{100}^2}} }}{{90 + 10}} = U\sqrt 2 $.(**)
Từ (*)(**) → $\frac{{{U_2}}}{{{U_1}}} = \frac{{U\sqrt 2 .10}}{U} = 10\sqrt 2 .$
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề ôn luyện thi THPT Quốc gia môn Lý số 4 có đáp án
Số câu hỏi: 40
Copyright © 2021 HOCTAP247
