Trang chủ
Đề thi & kiểm tra
Vật lý
Đề ôn luyện thi THPT Quốc gia môn Lý số 4 có đáp án
Mạch điện gồm điện trử R nối tiếp với hộp...
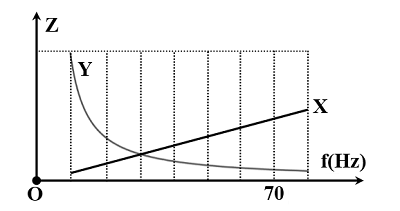
Mạch điện gồm điện trử R nối tiếp với hộp đen X và hộp đen Y. Biết X, Y là hai
Câu hỏi :
Mạch điện gồm điện trử R nối tiếp với hộp đen X và hộp đen Y. Biết X, Y là hai hộp có trở kháng phụ thuộc vào tần số như hình vẽ. Hiệu điện thế hiệu dung của hai đầu đoạn mạch là không đổi và bằng 220 V. Khi thay đổi tần số dòng điện thì công suất tiêu thụ điện năng lớn nhất của mạch điện là 200 W và khi đó điện áp trên X là 50 V. Khi đưa tần số mạch điện với giá trị là 70 Hz thì công suất của mạch gần giá trị nào nhất ?
A. 139 W
B. 168 W
C. 143 W
D. 173 W
* Đáp án
B
* Hướng dẫn giải
Từ đồ thị ta thấy đường X là một đường thẳng xiên góc nên X chứa cuộn dây ${Z_X}$ = L2πfĐồ thị Y có dạng là một hypebol nên Y chứa tụ điện ${Z_Y} = \frac{1}{{C2\pi f}}$
Tại giá trị f để ${Z_X} = {Z_Y}$ thì mạch xảy ra cộng hưởng, khi đó $f = {f_0} = \frac{3}{7}.70 = 30\,\,Hz$
Công suất tiêu thụ cực đại trên mạch là ${P_{\max }} = \frac{{{U^2}}}{R}$ ↔ $200 = \frac{{{{220}^2}}}{R}$ → R = 242 $\Omega $
Cường độ dòng điện trong mạch là $I = \frac{U}{R} = \frac{{220}}{{242}} = \frac{{10}}{{11}}\,\,A$
Cảm kháng và dung kháng tương ứng khi đó là ${Z_X} = {Z_Y} = \frac{{50}}{{\frac{{10}}{{11}}}} = 55\,\,\Omega $
Khi $f = \frac{7}{3}{f_0} = 70\,\,Hz$ thì dung kháng và cảm kháng tương ứng là
$Z{'_X} = \frac{7}{3}{Z_X} = \frac{{385}}{3}\,\,\Omega $
$Z{'_Y} = \frac{3}{7}{Z_Y} = \frac{3}{7}.55 = \frac{{165}}{7}\,\,\Omega $
Công suất tiêu thụ của mạch là $P = \frac{{{U^2}R}}{{{R^2} + \left( {Z{'_Y} - Z{'_X}} \right)}} = \frac{{{{220}^2}.242}}{{{{242}^2} + {{\left( {\frac{{385}}{3} - \frac{{165}}{7}} \right)}^2}}} = 168,43\,\,{\rm{W}}$.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề ôn luyện thi THPT Quốc gia môn Lý số 4 có đáp án
Số câu hỏi: 40
Copyright © 2021 HOCTAP247
