Hai nguồn sóng kết hợp S_1 và S_2cách nhau 2 m dao động điều hòa cùng pha, phát

* Hướng dẫn giải

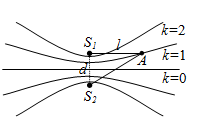
Điều kiện để tại A có cực đại giao thoa là hiệu đường đi từ A đến hai nguồn sóng phải bằng số nguyên lần bước sóng: ${d_2} - {d_1} = k\lambda \leftrightarrow \sqrt {{\ell ^2} + {d^2}} - \ell = k\lambda $. (Với k = 1, 2, 3...)
Khi l càng lớn đường ${S_1}A$ cắt các cực đại giao thoa có bậc càng nhỏ (k càng bé), vậy ứng với giá trị lớn nhất của l để tại A có cực đại nghĩa là tại A đường ${S_1}A$ cắt cực đại bậc 1 (k = 1).
→ $\sqrt {{\ell ^2} + 4} - \ell = 1 \to \ell = 1,5m.$