Trang chủ
Đề thi & kiểm tra
Vật lý
Đề ôn luyện thi THPT Quốc gia môn Lý số 4 có đáp án
Đặt vào hai đầu mạch điện có sơ đồ như...
Đặt vào hai đầu mạch điện có sơ đồ như hình vẽ một hiệu điện thế U_AB = 33V.
Câu hỏi :
Đặt vào hai đầu mạch điện có sơ đồ như hình vẽ một hiệu điện thế ${U_{AB}} = 33V$. Biết ${R_1} = 4\Omega ,{R_2} = {R_3} = 6\Omega ,{R_4} = 14\Omega $ và ampe kế có điện trở rất nhỏ không đáng kể. Số chỉ ampe kế là
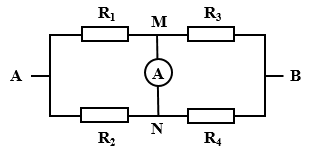
A. 5 A
B. 3 A
C. 3,5 A
D. 0,5 A
* Đáp án
D
* Hướng dẫn giải
Vì ${R_A} \simeq 0$ nên có thể chập M và N → mạch $\left( {{R_1}//{R_2}} \right)nt\left( {{R_3}//{R_4}} \right)$.Ta có ${R_{12}} = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = 2,4\Omega $; ${R_{34}} = \frac{{{R_3}.{R_4}}}{{{R_3} + {R_4}}} = 4,2\Omega $
→ ${R_{AB}} = {R_{12}} + {R_{34}} = 6,6\Omega .$
→ Cường độ dòng điện qua mạch chính $I = \frac{{{U_{AB}}}}{{{R_{AB}}}} = 5A$.
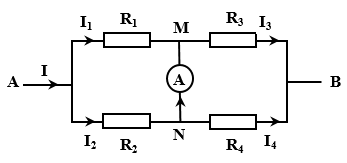
Chiều dòng điện qua các điện trở được biểu diễn như hình.
Ta có ${U_{AM}} = {U_1} = {U_2} = I.{R_{12}} = 12V.$
${U_{CB}} = {U_3} = {U_4} = I.{R_{34}} = 21V.$
→ ${I_1} = \frac{{{U_1}}}{{{R_1}}} = \frac{{12}}{4} = 3A;{I_3} = \frac{{{U_3}}}{{{R_3}}} = \frac{{21}}{6} = 3,5A.$
Nhận thấy ${I_3} > {I_1}$ → tại nút M có ${I_3} = {I_1} + {I_A}$ tức là dòng điện chạy qua ampe kế theo chiều từ N đến M.
Số chỉ ampe kế là ${I_A} = {I_3} - {I_1} = 0,5A.$
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề ôn luyện thi THPT Quốc gia môn Lý số 4 có đáp án
Số câu hỏi: 40
Copyright © 2021 HOCTAP247
