Trang chủ
Đề thi & kiểm tra
Vật lý
Đề ôn luyện thi THPT Quốc gia môn Lý số 5 có đáp án
Một sóng cơ truyền dọc theo theo trục Ox trên...
Một sóng cơ truyền dọc theo theo trục Ox trên một sợi dây đàn hồi rất dài với
Câu hỏi :
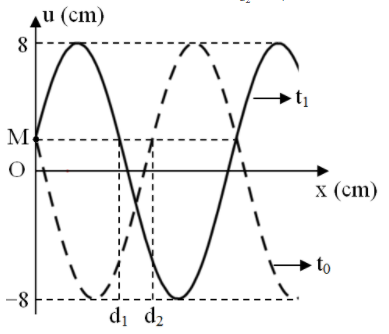
Một sóng cơ truyền dọc theo theo trục Ox trên một sợi dây đàn hồi rất dài với tần số f = 1/6 Hz. Tại thời điểm ${t_o}$ = 0 (s) và thời điểm ${t_1}$ (s), hình ảnh sợi dây có dạng như hình vẽ. Biết $\frac{{{d_1}}}{{{d_2}}} = \frac{5}{7}$, tốc độ của điểm M tại thời điểm t = ${t_1}$ + 4,25 s là
A. $\frac{{2\pi }}{3}$ cm/s
B. $\frac{{4\sqrt 2 \pi }}{3}$ cm/s
C. $\frac{{4\pi }}{{\sqrt 3 }}$ cm/s
D. $\frac{{4\pi }}{3}$ cm/s
* Đáp án
D
* Hướng dẫn giải
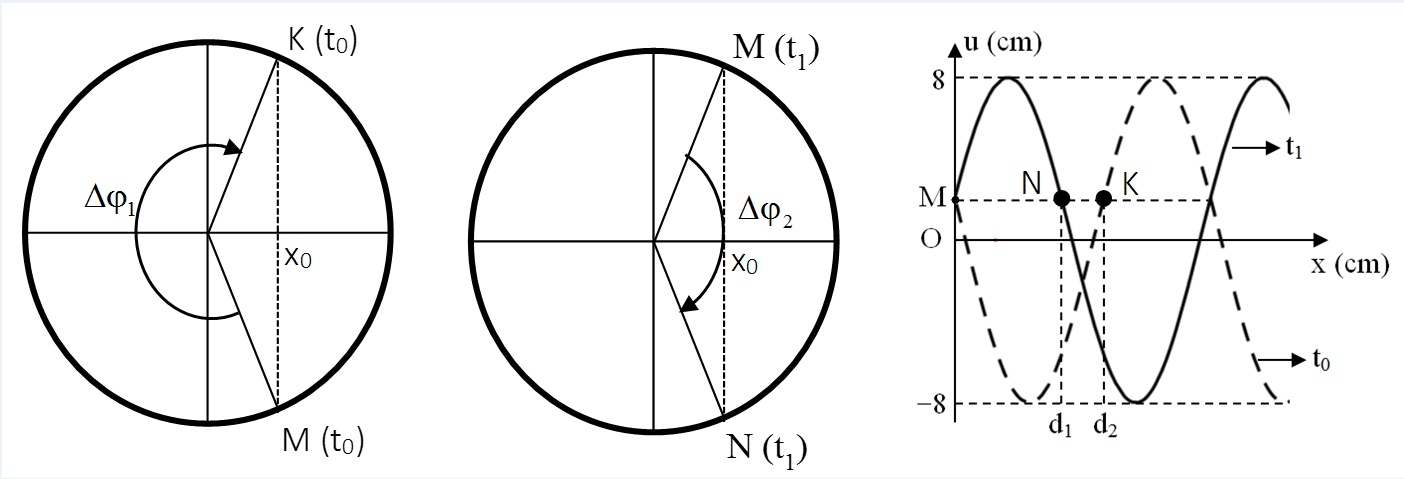
Xét ở thời điểm ${t_o}$: điểm K trễ pha hơn M một góc $\Delta {\varphi _1} = \frac{{2\pi {d_2}}}{\lambda }$.Xét thời điểm ${t_1}$: điểm N trễ pha hơn M một góc $\Delta {\varphi _2} = \frac{{2\pi {d_2}}}{\lambda }$.
→ $\frac{{\Delta {\varphi _1}}}{{\Delta {\varphi _2}}} = \frac{{{d_2}}}{{{d_1}}} = \frac{7}{5}$.
Mặt khác dựa vào 2 VTLG ta có $\Delta {\varphi _1} + \Delta {\varphi _2} = 2\pi $→ $\Delta {\varphi _1} = \frac{{7\pi }}{6};\Delta {\varphi _2} = \frac{{5\pi }}{6}$.
→ Tại thời điểm ${t_1}$ điểm M có pha là $\varphi = \frac{{5\pi }}{{12}}$.
Tốc độ của điểm M tại thời điểm t = ${t_1}$ + 4,25 là $v = \frac{{\omega A}}{2} = \frac{{4\pi }}{3}$ cm/s.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề ôn luyện thi THPT Quốc gia môn Lý số 5 có đáp án
Số câu hỏi: 40
Copyright © 2021 HOCTAP247
