Hai dao động điều hoà cùng phương, cùng tần số có phương trình x_1 =

Câu hỏi :

Hai dao động điều hoà cùng phương, cùng tần số có phương trình ${x_1} = {A_1}c{\rm{os}}\left( {\omega t - \pi /3} \right)cm$ và ${x_2} = 8c{\rm{os}}(\omega t + \varphi )cm$. Dao động tổng hợp có phương trình $x = A\cos \left( {\omega t - \pi /2} \right)cm$. Biên độ dao động tổng hợp có giá trị cực đại là

* Đáp án

B

* Hướng dẫn giải

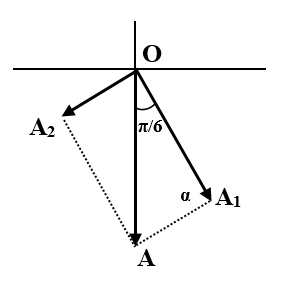
Áp dụng định lý hàm sin cho tam giác OA${A_1}$ ta được
$\begin{array}{l}
\frac{A}{{\sin \alpha }} = \frac{{{A_2}}}{{\sin \frac{\pi }{6}}} = 16 \Rightarrow A = 16\sin \alpha \le 16\\
\Rightarrow {A_{m{\rm{ax}}}} = 16cm
\end{array}$