Trang chủ
Lớp 8
Toán Lớp 8 SGK Cũ
Chương 4: Hình Lăng Trụ Đứng. Hình Chóp Đều
Bài tập 61 trang 150 SBT Toán 8 Tập 2
Bài tập 61 trang 150 SBT Toán 8 Tập 2
Lý thuyết
Bài tập
Câu hỏi:
Bài tập 61 trang 150 SBT Toán 8 Tập 2
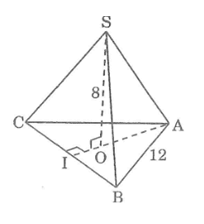
Hình chóp đều S.ABC có cạnh đáy bằng a=12cm,chiều cao h=8cm.Hãy tính diện tích xung quanh của hình chóp đó
Kẻ AO kéo dài cắt BC tại I
Ta có: AI ⊥ BC (tính chất tam giác đều)
BI = IC = \(\frac{1}{2}\) BC
Áp dụng định lí pi-ta-go vào tam giác vuông AIB,ta có:
AB2 =BI2+AI2
Suy ra: AI2 = AB2- BI2 =122 - 62=108
AI = \(\sqrt {108} \) cm
Vì tam giác ABC đều nên O là trọng tâm của tam giác ABC
Ta có: OI = \(\frac{1}{3}\).AI = \(\frac{1}{3}\).\(\sqrt {108} \) cm
Áp dụng định lí pi-ta-go vào tam giác vuông SOI ta có:
SI2= SO2 + OI2 = 8 + \(\frac{1}{9}\) .108 = 76
SI = \(\sqrt {76} \) cm
Vậy
\(\begin{array}{l}
{S_{xq}} = P.d\\
= \frac{{12.3}}{2}.\sqrt {176} \\
= 18\sqrt {76} \left( {cm} \right)
\end{array}\)
-- Mod Toán 8
Copyright © 2021 HOCTAP247