Bài tập 48 trang 125 SGK Toán 8 Tập 2
Bài tập 48 trang 125 SGK Toán 8 Tập 2
Tính diện tích toàn phần của:
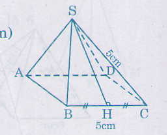
a) Hình chóp tứ giác đều, biết cạnh đáy a = 5cm, cạnh bên b = 5cm, \(\sqrt{18,75} \approx 4,33\)
b) Hình chóp lục giác đều, biết cạnh đáy a = 6cm, cạnh bên b = 5cm, \(\sqrt{3} \approx 1,73\)
Câu a:
Ta có các mặt bên của hình chóp đều là những tam giác đều cạnh 5cm. Đường cao của mỗi mặt bên :
SH =
= = √18,75 ≈ 4,33 (cm)
Diện tích xung quanh hình chóp:
Sxq = p.d = .5.4. 4,33 = 43,3 (cm2)
Diện tích đáy hình chóp:
Sđ = a 2 = 52 = 25(cm2)
Diện tích toàn phần hình chóp:
Stp = Sxq + Sđ = 43,3 + 25 = 68,3 (cm2)
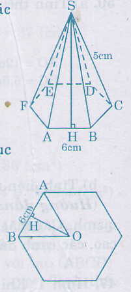
Câu b:
Mặt bên của hình chóp lục giác đều là tam giác cân có cạnh bên 5cm, cạnh đáy 6cm.
Đường cao SH của mặt bên là :
SH = =
= √16 = 4 (cm)
Diện tích xung quanh hình chóp:
Sxq = p.d = .6.6 .4 =72 (cm2)
Đáy của hình chóp là lục giác đều. Diện tích lục giác bằng 6 lần diện tích tam giác đều ABO.
Chiều cao của tam giác đều là:
OH = =
= √27 ≈ 5,2 (cm)
Diện tích đáy hình chóp:
Sđ = 6..6.5,2 = 93,6 (cm2)
Diện tích toàn phần hình chóp:
Stp = Sxq + Sđ =72 + 93,6 =165,6 (cm2)
-- Mod Toán 8
Copyright © 2021 HOCTAP247
