Bài tập 72 trang 153 SBT Toán 8 Tập 2
Bài tập 72 trang 153 SBT Toán 8 Tập 2
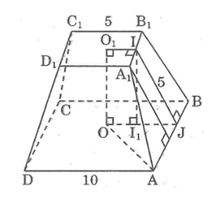
Cho hình chóp cụt tứ giác đều ABCD.A1B1C1D1 có các cạnh đáy 5cm và 10cm, đường cao mặt bên bằng 5cm. Hãy tính:
a) Diện tích xung quanh của hình chóp cụt.
b) Tính cạnh bên và đường cao hình chóp cụt.
Diện rích một mặt bên là hình thang bằng:
S =\(\frac{1}{2}\) (5 +10).5=37,5 (cm2)
Diện tích xung quanh của hình chóp
cụt đều là: Sxq =4.3,75 = 150 (cm2)
Kẻ A1H ⊥ AB, ta có:
A1I = 2,5cm; AJ = 5cm
Suy ra: AH = 2,5cm
Áp dụng định lí Pi-ta-go vào tam giác vuông A1HA, ta có:
A1A2 = A1H2 + AH2 = 52 + 2,52 = 31,25
Suy ra: A1A = \(\sqrt {31,25} \) ≈ 5,59 (cm)
Ta có: O1I = 2,5; OJ = 5cm.
Kẻ II1 ⊥ OJ, suy ra I1J = 2,5.
Áp dụng định kí Pi-ta-go vào tam giác vuông II1J, ta có:
IJ2 = II12 + I1J2
Suy ra: II12 = IJ2 – I1J2 = 52 – 2,52 = 18,75
Suy ra: II1 = \(\sqrt {18,75} \) ≈ 4,33 (cm)
Vậy O1O = II1 = 4,33 (cm)
-- Mod Toán 8
Copyright © 2021 HOCTAP247