Trang chủ
Lớp 8
Toán Lớp 8 SGK Cũ
Chương 4: Hình Lăng Trụ Đứng. Hình Chóp Đều
Bài tập 71 trang 153 SBT Toán 8 Tập 2
Bài tập 71 trang 153 SBT Toán 8 Tập 2
Lý thuyết
Bài tập
Câu hỏi:
Bài tập 71 trang 153 SBT Toán 8 Tập 2
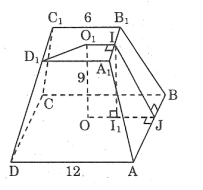
Tính diện tích toàn phần của hình chóp cụt đều theo các kích thước cho trên hình
Ta có: A1D1 =6 => O1I=3
AD=12 => OJ=6
Kẻ II1 ⊥ OJ ta có: I1J=3
Áp dụng định lí pi-ta-go vào
tam giác vuông II1J,ta có:
IJ2= II12 + I1J2 = 92 + 32 =90
Suy ra: IJ = \(\sqrt {90} \)
Diện tích mặt một bên là một hình thang bằng: S =\(\frac{1}{2}\). (6+12).\(\sqrt {90} \) =9\(\sqrt {90} \) (đvdt)
Diện tích xung quanh bằng : Sxq = 4.9\(\sqrt {90} \) =36\(\sqrt {90} \) (đvdt)
Diện tích đáy trên bằng: S = 6.6=36(đvdt)
Diện tích đáy dưới bằng: S=12.12=144 (đvdt)
Diện tích toàn phần của hình chóp cụt bằng: STP = 36\(\sqrt {90} \) +36+144=(36\(\sqrt {90} \) +180) (đvdt)
-- Mod Toán 8
Copyright © 2021 HOCTAP247