Bài tập 46 trang 124 SGK Toán 8 Tập 2
Bài tập 46 trang 124 SGK Toán 8 Tập 2
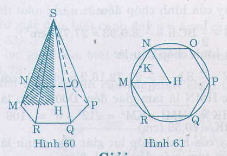
S.MNOPQR là một hình chóp lục giác đều (h.60). Bán kính đường tròn ngoại tiếp đáy (đường tròn tâm H, đi qua sáu đỉnh của đáy) HM = 12cm(h.61), chiều cao SH = 35cm. Hãy tính:
a)Diện tích đáy và thể tích của hình chóp (biết √108 ≈ 10,39)
b) Độ dài cạnh bên SM và diện tích toàn phần của hình chóp (biết √1333 ≈ 36,51).
Câu a:
Tam giác HMN là tam giác đều.
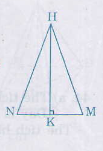
Đường cao là:
HK = =
= √108 ≈ 10,39(cm)
Diện tích đáy của hình chóp lục giác đều chính là 6 lần diện tích của tam giác đều HMN. Nên
Sđ = 6.. MN.HK = 6.
. 12 .10,39 = 374,04(cm2)
Thể tích của hình chóp:
V = . Sđ . SH =
. 374,04 . 35 = 4363,8(cm3)
Câu b:
=
= √1369 = 37 (cm)
Đường cao của mỗi mặt bên là :
h = SK =
= = √1333 ≈ 36,51 (cm)
Diện tích xung quanh hình chóp là :
Sxq = . p.d =
.6. MK .SK =
.6.12. 36,51 = 1314,36(cm2)
Diện tích toàn phần : Stp = Sxq + Sđ = 1314,36 + 374,04 = 1688,4(cm2)
-- Mod Toán 8
Copyright © 2021 HOCTAP247
