Trang chủ
Lớp 9
Toán Lớp 9 SGK Cũ
Ôn tập chương IV - Hàm số y = ax^2 (a ≠ 0). Phương trình bậc hai một ẩn
Giải bài 55 trang 63 - Sách giáo khoa Toán 9 tập 2
Giải bài 55 trang 63 - Sách giáo khoa Toán 9 tập 2
Lý thuyết
Bài tập
Mục lục
Tóm tắt bài
Đề bài
Cho phương trình: \(x^2-x-2=0\) = 0.
a) Giải phương trình.
b) Vẽ hai đồ thị y = \(x^2\) và y = x + 2 trên cùng một hệ trục tọa độ.
c) Chứng tỏ rằng hai nghiệm tìm được trong câu a) là hoành độ giao điểm của hai đồ thị.
Hướng dẫn giải
Giải:
a) \(\Delta = (-1)^2 - 4.1.(-2)=9\)
Phương trình có hai nghiệm:
\(x_1 = \dfrac{1-3}{2}= -1; x_2 = \dfrac{1+3}{2}\)
Vậy S= { -1;2}
b) Lập bảng giá trị:
| x | -2 | -1 | 0 | 1 | 2 |
| \(y =x^2\) | 4 | 1 | 0 | 1 | 4 |
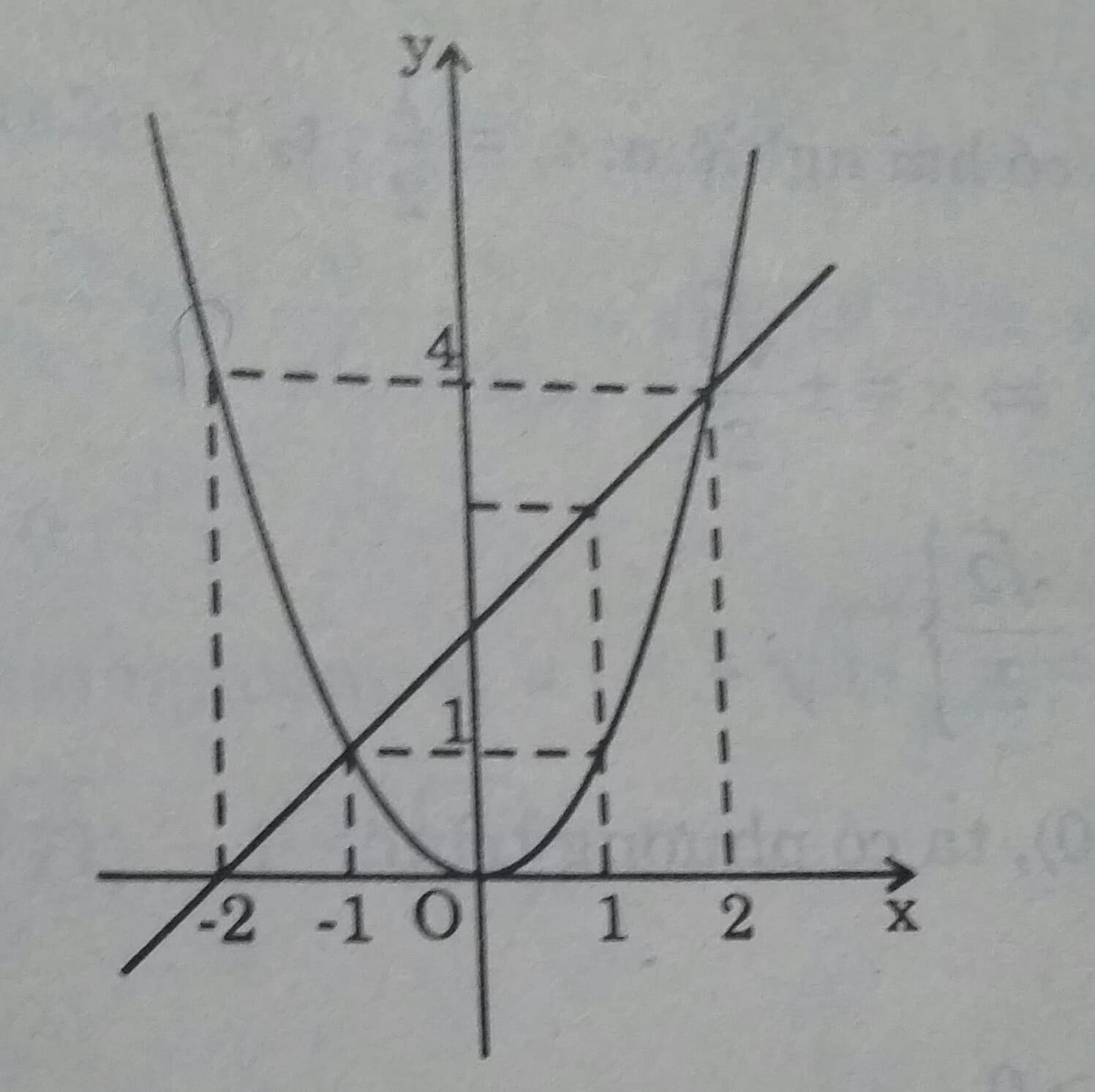
Đường thẳng y = x+2 là đường thẳng đi qua hai điểm (0;2) và (-2;0)
c) Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình:
\(x^2 = x+2 \Leftrightarrow x^2 -x-2=0 \Leftrightarrow x= -1 \ hoặc \ x = 2\)
Copyright © 2021 HOCTAP247
