Hệ phương trình mũ logarit
Câu 1 :
Giải hệ phương trình: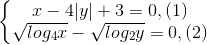
A (x;y) = (1;1) ; (x;y) = (3;9)
B (x;y) = (9;3)
C (x;y) = (3;9)
D (x;y) = (1;1) ; (x;y) = (9;3)
Câu 2 :
Giải hệ phương trình: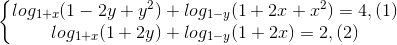
A 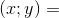
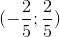
B 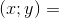
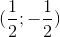
C 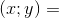
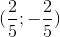
D 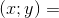
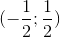
Câu 3 :
Giải hệ phương trình: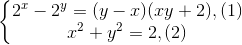
A (x ; y ) = (-1; -1 )
B (x; y) = (1;1)
C cả A, B
D (x; y) = (1;1); (x; y) = (-1;1)
Câu 4 :
Giải hệ phương trình: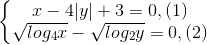
A (x;y) = (1;1) ; (x;y) = (3;9)
B (x;y) = (9;3)
C (x;y) = (3;9)
D (x;y) = (1;1) ; (x;y) = (9;3)
Câu 5 :
Giải hệ phương trình: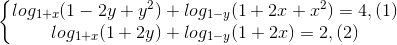
A 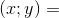
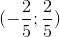
B 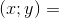
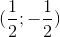
C 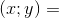
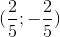
D 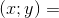
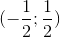
Câu 6 :
Giải hệ phương trình: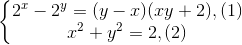
A (x ; y ) = (-1; -1 )
B (x; y) = (1;1)
C cả A, B
D (x; y) = (1;1); (x; y) = (-1;1)
Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).
Copyright © 2021 HOCTAP247
