Tổng hợp chuyên đề mũ logarit
Câu 1 :
giải phương trình sau: 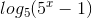 .
.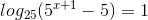
A 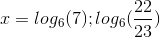
B x=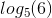 ; x=
; x=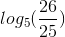
C 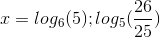
D x=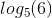 ;x=
;x=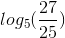
Câu 2 :
Giải bất phương trình :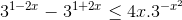
A x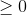
B x>0
C x<0
D x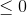
Câu 3 :
giải hệ phương trình 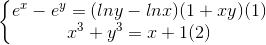
A (x;y)=(-1;-1)
B (x,y)=(1;-1)
C (x;y)=(0;0)
D (x,y)=(1;1)
Câu 4 :
giải phương trình sau: 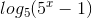 .
.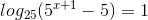
A 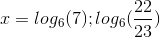
B x=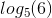 ; x=
; x=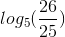
C 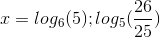
D x=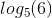 ;x=
;x=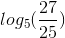
Câu 5 :
Giải bất phương trình :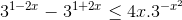
A x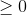
B x>0
C x<0
D x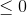
Câu 6 :
giải hệ phương trình 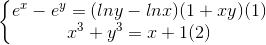
A (x;y)=(-1;-1)
B (x,y)=(1;-1)
C (x;y)=(0;0)
D (x,y)=(1;1)
Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).
Copyright © 2021 HOCTAP247
