Bất phương trình logarit

Câu 1 : Giải bất phương trình sau: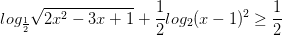 $\dpi{100} log_{\frac{1}{2}}\sqrt{2x^{2}-3x+1}+\frac{1}{2}log_{2}(x-1)^{2}\geq \frac{1}{2}$

A x < $\dpi{100} \frac{1}{2}$

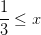
B $\dpi{100} \frac{1}{3}\leq x$

C $\dpi{100} \frac{1}{3}$ < x < $\dpi{100} \frac{1}{2}$

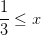D $\dpi{100} \frac{1}{3}\leq x$ < $\dpi{100} \frac{1}{2}$

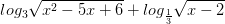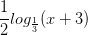
Câu 2 : Giải bất phương trình $\dpi{100} log_{3}\sqrt{x^{2}-5x+6}+log_{\frac{1}{3}}\sqrt{x-2}$ > $\dpi{100} \frac{1}{2}log_{\frac{1}{3}}(x+3)$

A x < 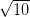$\dpi{100} \sqrt{10}$

B x 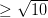$\dpi{100} \geq \sqrt{10}$

C x > 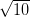$\dpi{100} \sqrt{10}$

D x 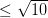$\dpi{100} \leq \sqrt{10}$

Câu 3 : Giải bất phương trình: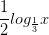 $\dpi{100} \frac{1}{2}log_{\frac{1}{3}}x$ < $\dpi{100} log_{\frac{1}{3}}(1+\sqrt[3]{x-1})$ (1)

A x > 9

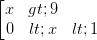B $\dpi{100} \left [ \begin{matrix} x>9 & \\ 0 < x < 1 & \end{matrix}$ (Chú ý : chữ gt nghĩa là dấu > ; chữ lt là dấu < )

C 0 < x < 1

D x < 1 hoặc x > 9

Câu 4 : Giải bất phương trình sau: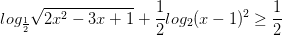 $\dpi{100} log_{\frac{1}{2}}\sqrt{2x^{2}-3x+1}+\frac{1}{2}log_{2}(x-1)^{2}\geq \frac{1}{2}$

A x < $\dpi{100} \frac{1}{2}$

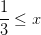
B $\dpi{100} \frac{1}{3}\leq x$

C $\dpi{100} \frac{1}{3}$ < x < $\dpi{100} \frac{1}{2}$

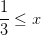D $\dpi{100} \frac{1}{3}\leq x$ < $\dpi{100} \frac{1}{2}$

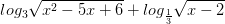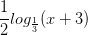
Câu 5 : Giải bất phương trình $\dpi{100} log_{3}\sqrt{x^{2}-5x+6}+log_{\frac{1}{3}}\sqrt{x-2}$ > $\dpi{100} \frac{1}{2}log_{\frac{1}{3}}(x+3)$

A x < 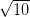$\dpi{100} \sqrt{10}$

B x 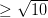$\dpi{100} \geq \sqrt{10}$

C x > 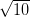$\dpi{100} \sqrt{10}$

D x 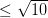$\dpi{100} \leq \sqrt{10}$

Câu 6 : Giải bất phương trình: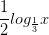 $\dpi{100} \frac{1}{2}log_{\frac{1}{3}}x$ < $\dpi{100} log_{\frac{1}{3}}(1+\sqrt[3]{x-1})$ (1)

A x > 9

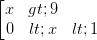B $\dpi{100} \left [ \begin{matrix} x>9 & \\ 0 < x < 1 & \end{matrix}$ (Chú ý : chữ gt nghĩa là dấu > ; chữ lt là dấu < )

C 0 < x < 1

D x < 1 hoặc x > 9

Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).

Bất phương trình logarit

Toán học - Lớp 12

Trắc nghiệm Toán 12 Chương 2 Bài 1 Lũy thừa

Trắc nghiệm Toán 12 Chương 2 Bài 2 Hàm số lũy thừa

Trắc nghiệm Toán 12 Chương 2 Bài 4 Hàm số mũ và hàm số lôgarit

Trắc nghiệm Toán 12 Chương 2 Bài 5 Phương trình mũ và phương trình lôgarit

Trắc nghiệm Toán 12 Chương 2 Bài 6 Bất phương trình mũ và bất phương trình lôgarit

Trắc nghiệm Toán 12 Chương 3 Bài 1 Nguyên hàm

Trắc nghiệm Toán 12 Chương 3 Bài 2 Tích phân

Trắc nghiệm Toán 12 Chương 3 Bài 3 Ứng dụng của tích phân trong hình học

Trắc nghiệm Toán 12 Bài 1 Số phức

Trắc nghiệm Toán 12 Bài 2 Cộng, trừ và nhân số phức

Trắc nghiệm Toán 12 Chương 4 Bài 3 Phép chia số phức

Trắc nghiệm Toán 12 Chương 4 Bài 4 Phương trình bậc hai với hệ số thực

Trắc nghiệm Toán 12 Chương 1 Bài 5 Khảo sát sự biến thiên và vẽ đồ thị của hàm số

Trắc nghiệm Hình học 12 Chương 1 Bài 1 Khái niệm về khối đa diện

Trắc nghiệm Hình học 12 Chương 1 Bài 2 Khối đa diện lồi và khối đa diện đều

Trắc nghiệm Hình học 12 Chương 1 Bài 3 Khái niệm về thể tích khối đa diện

Trắc nghiệm Hình học 12 Chương 2 Bài 2 Khái niệm về mặt tròn xoay

Trắc nghiệm Hình học 12 Chương 2 Bài 2 Mặt cầu

Trắc nghiệm Hình học 12 Bài 1 Hệ tọa độ trong không gian

Trắc nghiệm Hình học 12 Chương 3 Bài 2 Phương trình mặt phẳng

Trắc nghiệm Hình học 12 Chương 3 Bài 3 Phương trình đường thẳng trong không gian

Trắc nghiệm Hình học 12 Chương 3 Phương pháp tọa độ trong không gian

Trắc nghiệm Hình học 12 Chương 1 Khối đa diện

Trắc nghiệm Toán 12 Chương 4 Số phức

Trắc nghiệm Toán 12 Chương 3 Nguyên hàm, tích phân và ứng dụng

Câu 1 : Giải bất phương trình sau: $\dpi{100} log_{\frac{1}{2}}\sqrt{2x^{2}-3x+1}+\frac{1}{2}log_{2}(x-1)^{2}\geq \frac{1}{2}$

Câu 2 : Giải bất phương trình $\dpi{100} log_{3}\sqrt{x^{2}-5x+6}+log_{\frac{1}{3}}\sqrt{x-2}$ > $\dpi{100} \frac{1}{2}log_{\frac{1}{3}}(x+3)$

Câu 3 : Giải bất phương trình: $\dpi{100} \frac{1}{2}log_{\frac{1}{3}}x$ < $\dpi{100} log_{\frac{1}{3}}(1+\sqrt[3]{x-1})$ (1)

Câu 4 : Giải bất phương trình sau: $\dpi{100} log_{\frac{1}{2}}\sqrt{2x^{2}-3x+1}+\frac{1}{2}log_{2}(x-1)^{2}\geq \frac{1}{2}$

Câu 5 : Giải bất phương trình $\dpi{100} log_{3}\sqrt{x^{2}-5x+6}+log_{\frac{1}{3}}\sqrt{x-2}$ > $\dpi{100} \frac{1}{2}log_{\frac{1}{3}}(x+3)$

Câu 6 : Giải bất phương trình: $\dpi{100} \frac{1}{2}log_{\frac{1}{3}}x$ < $\dpi{100} log_{\frac{1}{3}}(1+\sqrt[3]{x-1})$ (1)

Lớp 12

Toán học

Toán học - Lớp 12

Bất phương trình logarit

Câu 1 : Giải bất phương trình sau:

Câu 2 : Giải bất phương trình >

Câu 3 : Giải bất phương trình: < (1)

Câu 4 : Giải bất phương trình sau:

Câu 5 : Giải bất phương trình >

Câu 6 : Giải bất phương trình: < (1)

Câu 1 : Giải bất phương trình sau: $\dpi{100} log_{\frac{1}{2}}\sqrt{2x^{2}-3x+1}+\frac{1}{2}log_{2}(x-1)^{2}\geq \frac{1}{2}$

Câu 2 : Giải bất phương trình $\dpi{100} log_{3}\sqrt{x^{2}-5x+6}+log_{\frac{1}{3}}\sqrt{x-2}$ > $\dpi{100} \frac{1}{2}log_{\frac{1}{3}}(x+3)$

Câu 3 : Giải bất phương trình: $\dpi{100} \frac{1}{2}log_{\frac{1}{3}}x$ < $\dpi{100} log_{\frac{1}{3}}(1+\sqrt[3]{x-1})$ (1)

Câu 4 : Giải bất phương trình sau: $\dpi{100} log_{\frac{1}{2}}\sqrt{2x^{2}-3x+1}+\frac{1}{2}log_{2}(x-1)^{2}\geq \frac{1}{2}$

Câu 5 : Giải bất phương trình $\dpi{100} log_{3}\sqrt{x^{2}-5x+6}+log_{\frac{1}{3}}\sqrt{x-2}$ > $\dpi{100} \frac{1}{2}log_{\frac{1}{3}}(x+3)$

Câu 6 : Giải bất phương trình: $\dpi{100} \frac{1}{2}log_{\frac{1}{3}}x$ < $\dpi{100} log_{\frac{1}{3}}(1+\sqrt[3]{x-1})$ (1)